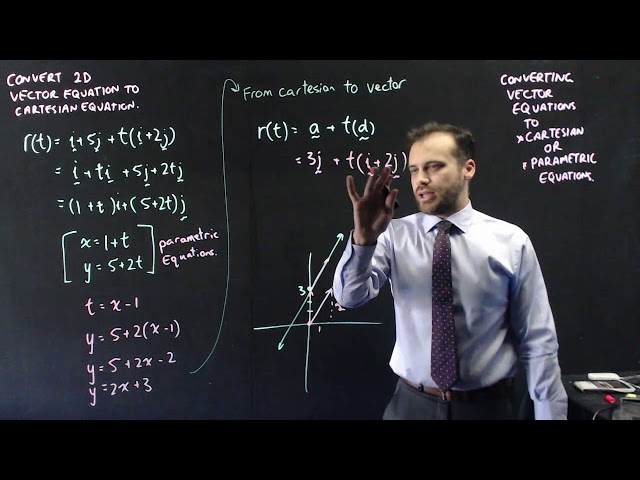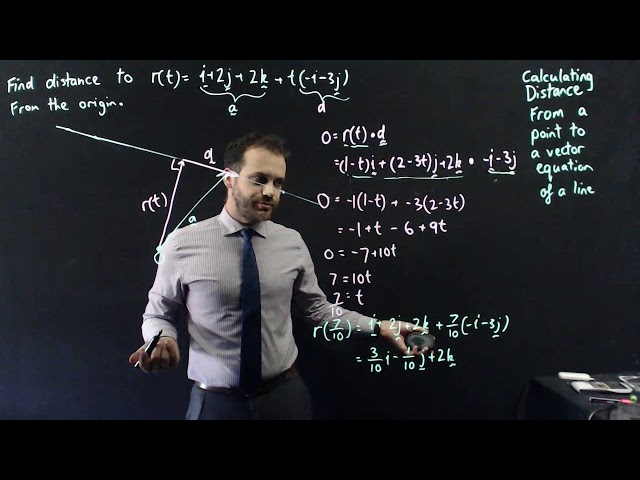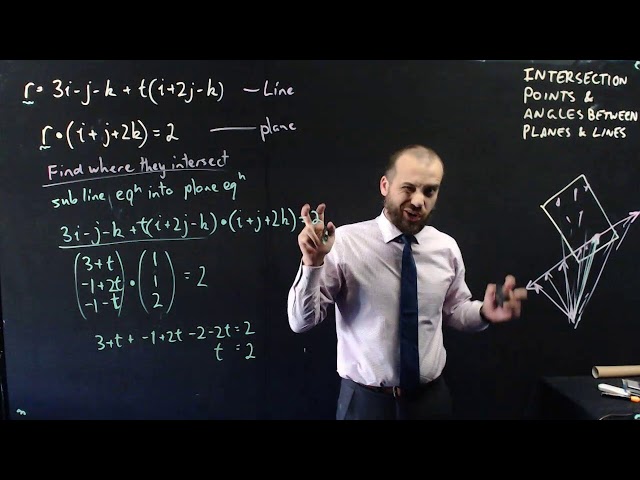Unit 3
Specialist Mathematics (Western Australia)
Topic 1: Complex Numbers
-

Complex Numbers: A Very Fast Recap of i, Operations, Conjugates, Argand Diagrams & Modulus
-

Complex Numbers: Polar Form: Fast Recap including Operations on Polar Form.
-

Factorising & Solving quadratics over C
-

Conjugate root theorem: What it is and Proof
-

Factor & Remainder Theorems: Proof and Application
-

Factorising Polynomials over C worked examples
-

Calculating Roots of a complex number using De Moivre’s Theorem
-

Roots of Unity
-

Sketching Subsets of the complex Plane
Topic 2: Functions & Sketching Graphs (Coming Soon)
Coming Soon
Topic 3: Real and Complex Numbers
-

15 Vector Questions you should know how to do by the end of year 11
-

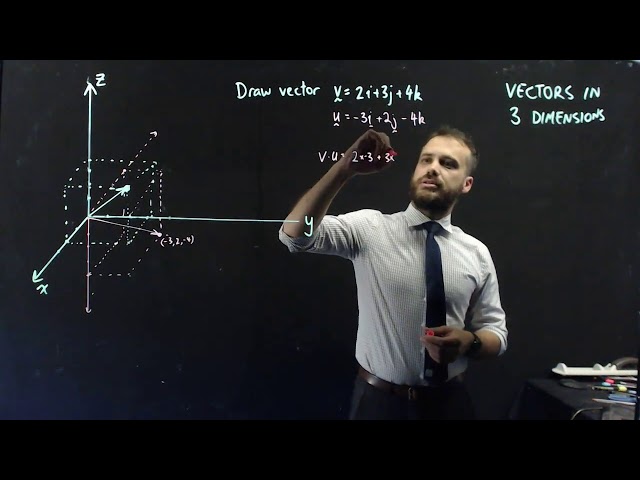
An Introduction to vectors in 3 dimensions
-

Converting 3D Vectors between Cartesian and Polar forms
-

Scalar or Dot Product in 3 Dimensions
-

Vector Functions Introduction and converting vector functions to cartesian functions
-

Converting Vector Equations to Cartesian Equations using trigonometric Identities
-

Vector equations and finding collision points
-

Vector Equations of Lines
-

Converting Vector equations to cartesian form and parametric equations
-

Parallel and perpendicular vector equations
-

Calculating distance from a point to a vector equation of a line
-

Vectors: Line of intersection & the angle between two planes
-

The Vector Product (Cross Product)
-

Vector Equation of a plane fully explained and shown graphically
-

Finding equations of planes: Three worked examples
-

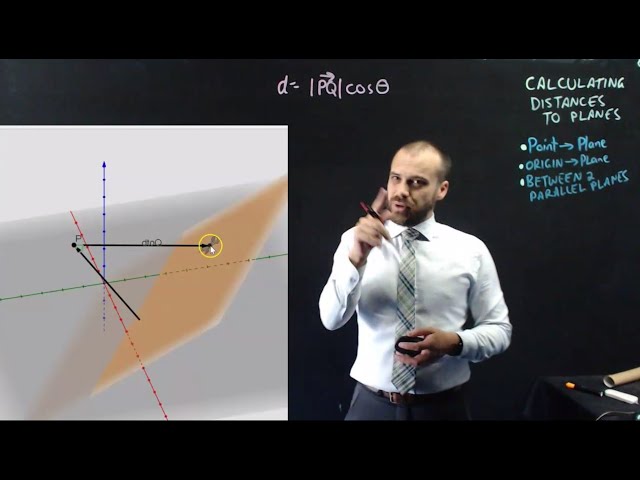
Vectors: Calculating the distance from a point to a plane or a plane to a plane
-

Vectors Intersection points between lines and planes and the angle between a line and a plane
-

Vector Calculations & 3D Graphing on the Casio FX CG50AU
-

Intersections of 3D Lines, Skew Lines and angles between lines
-

Equation of spheres in cartesian and vector form
-

The geometric interpretation of systems of linear equations in 2 & 3 dimensions
-

Using Matrix Algebra to find an intersection point of 3 planes
-

Solving Simultaneous Equations on the Casio FX CG50AU
-

Gaussian elimination: part 1
-

Guassian Elimination Part 2 Systems with lines as solutions
-

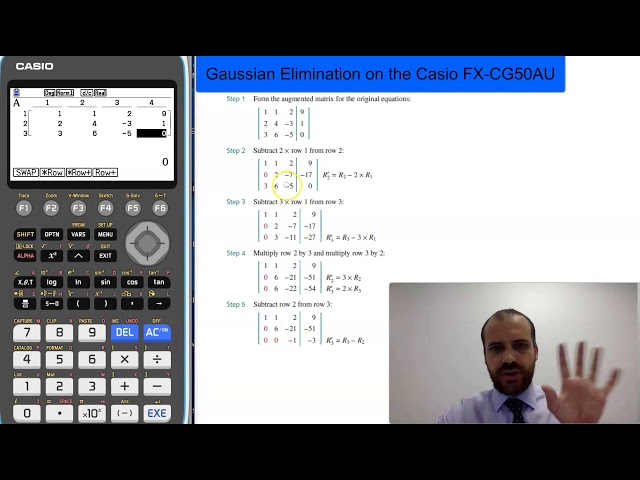
Gaussian Elimination on the Casio FX CG50AU
-

Gaussian Elimination part 3: systems resulting in No Solution
-

Gaussian Elimination part 4 Finding the equation of a plane resulting in an intersection
-

Vector Calculus Displacement, velocity Acceleration
-

Vector Calculus Anti differentiation worked example
-

Vector Calculus Differentiation worked examples
-

Vector Calculus Motion in a straight line
-

Vector Calculus Projectile Motion Calculating Launch Angle
-

Uniform Circular Motion Introduction
-

Uniform Circular Motion worked example