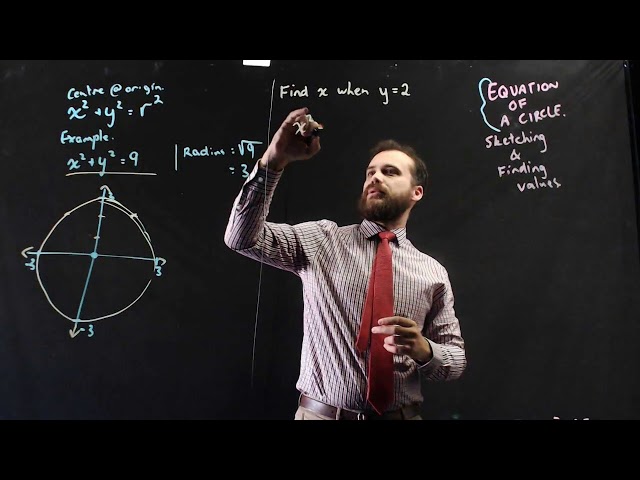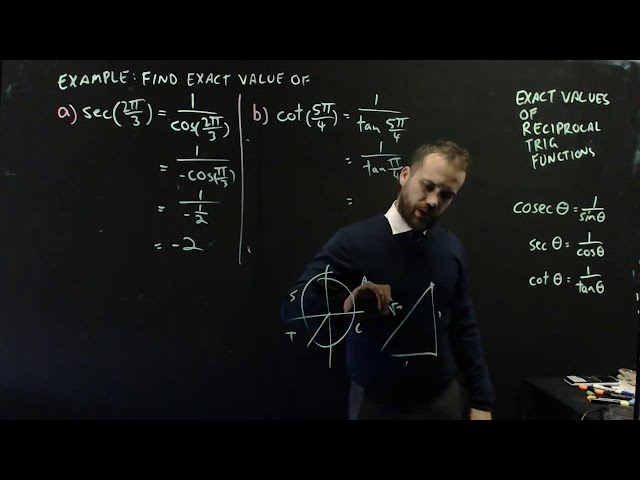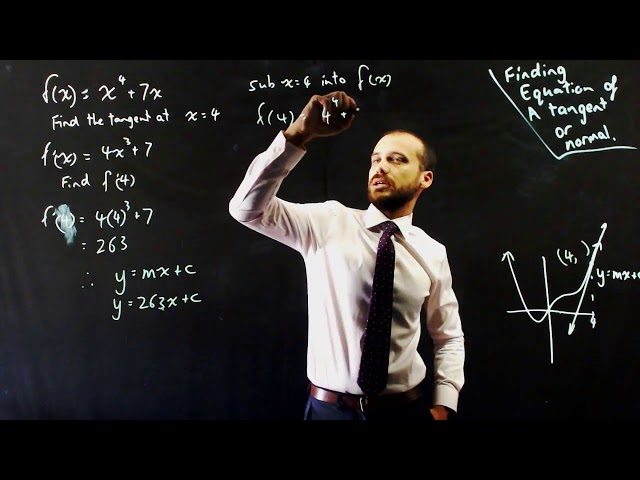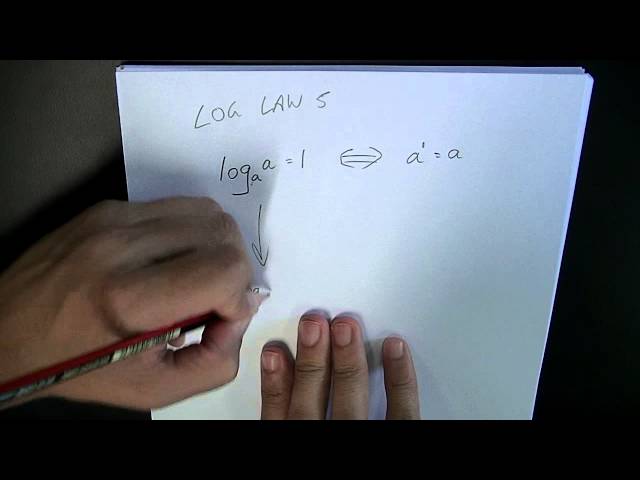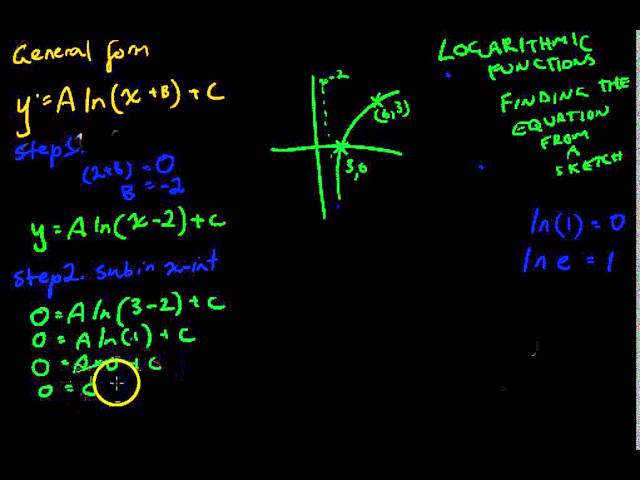Year 11
Mathematics Advanced (New South Wales)
MA-F1: Working With Functions
F1.1: Algebraic Techniques
-

Introduction to index laws and using them to simplify algebraic expressions
-

Index Law 1 – multiplication of indices
-

Index Law 2 – dividing indices
-

Index Law 3 – raising to the power of zero
-

Index Law 4 – Raising a power to another power
-

Index Law 5 – worked examples using the fifth index law
-

Index Law 6 – expanding brackets around a fraction raised to a power
-

Index law 7 Negative Indices – converting Negative indices into positive indices using fractions
-

Index Law 8 Fractional Indices – moving from index form to radical form
-

Index Laws equating bases to solve for unknown exponent or power part 1
-

Index Laws equating bases to solve for unknown exponent or power part 2
-

Index Laws Negative bases
-

Index Laws Fractional indices
-

Harder Indicial Equations
-

Solving Indicial equations
-

Indicial equations super hard quadratic action
-

Indicial equations The hardest one
-

Surds what is a surd
-

Simplifying surds
-

Simplifying Surds
-

Surds simplifying algebraic surds
-

Surds adding and subtracting surds
-

Adding and subtracting surds
-

Multiplying surds
-

Multiplying surds and the distributive law
-

Surds square numbers
-

Surds dividing
-

Dividing Surds
-

Solving Quadratics 3 ways
-

The quadratic formula and the discriminant
-

Completing the square part 1
-

Completing the square part 2
-

Solving by completing the square
-

Algebraic fractions cancelling common factors
-

Algebraic fractions multiplying and dividing
-

Algebraic fractions adding and subtracting
-

Algebraic fractions adding and subtracting part 2
-

Algebraic fractions adding and subtracting part 3
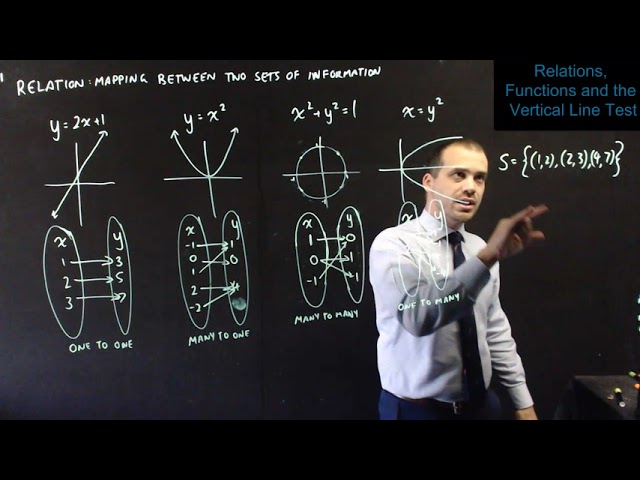
F1.2: Introduction to Functions
F1.3: Linear, Quadratic and Cubic Functions
-

Find x and y values from a graph
-

Plotting Linear graphs
-

Equations of horizontal and vertical lines
-

The equation of a line y = mx + c
-

Determining the rule of a linear graph
-

Anatomy of a linear graph
-

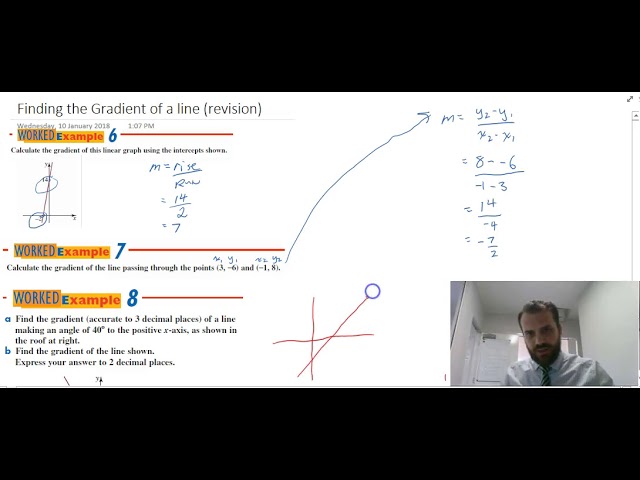
Finding the gradient of a line revision
-

Parallel lines and their gradients
-

Perpendicular lines and their gradients
-

3 forms of the quadratic equation
-

The quadratic formula and the discriminant
-

solving simultaneous equations using quadratic and linear graphs
-

Modelling and problem solving with quadratics
-

Cubics quartics and greater polynomials in Turning Point Form
-

Factor form of Quadratics cubics and Quartics
-

Factorise solve and sketch a cubic
F1.4: Further Functions and Relations
-

Factor form of Quadratics cubics and Quartics
-

Cubics quartics and greater polynomials in Turning Point Form
-

Finding a linear factor of a polynomial
-

Intersecting Functions
-

Direct and Indirect Proportion
-

Equations of hyperbola and sketching
-

Sketching Hyperbolas and why there’s an asymptote
-

Finding equation of reciprocal function from sketch
-

The modulus or absolute value function introduction
-

The modulus or absolute value solving equations
-

Absolute Value Functions
-

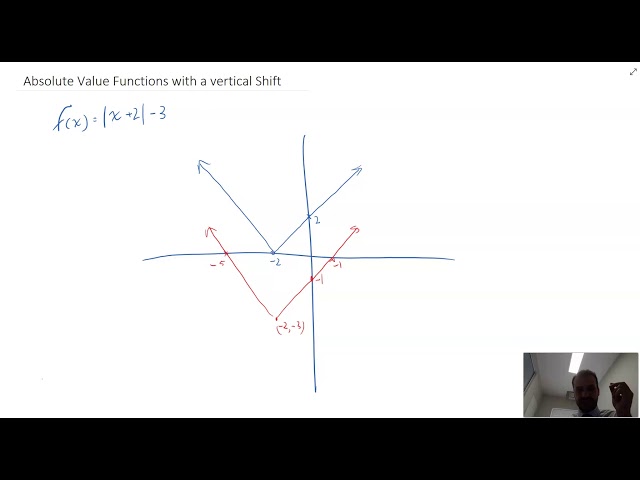
Sketch Absolute Value Functions with a vertical shift
-

Sketching an absolute value function worked example
-

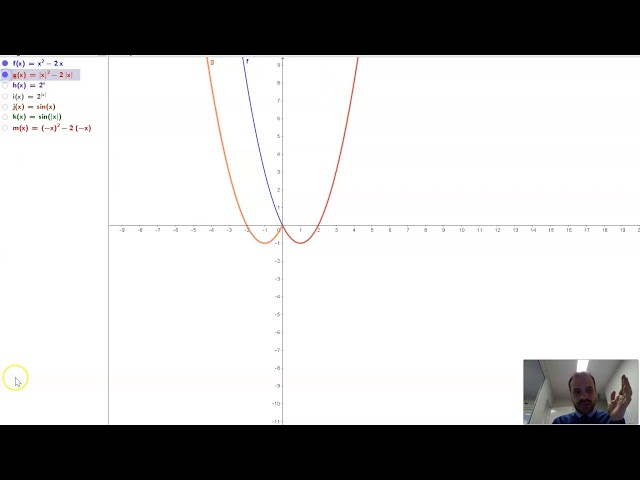
Reflecting Functions in the y axis using absolute value functions
-

Function Transformations intro
-

Functions Transformation fx+a
-

Function transformation f(x+a)
-

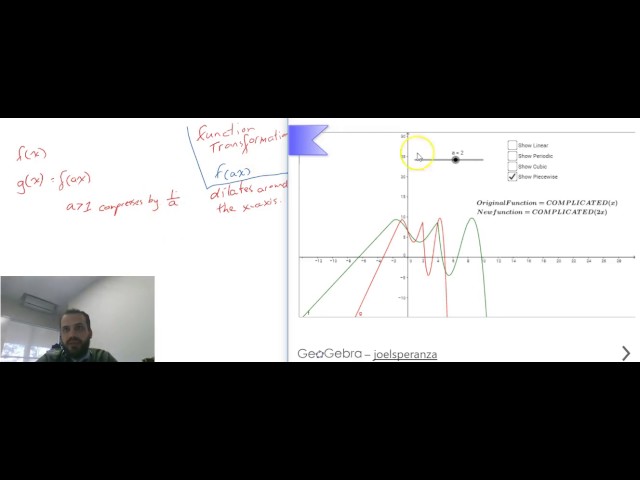
Functions transformations f(ax)
-

Sketching circles and finding equations of circles
-

Equation of a circle sketching and finding coordinates
MA-T1: Trigonometry And Measure of Angles
T1.1: Trigonometry
T1.2: Radians
-

Introduction to Radians
-

Converting Radians to Degrees and Degrees to Radians
-

Radians quick angles
-

Standard triangles
-

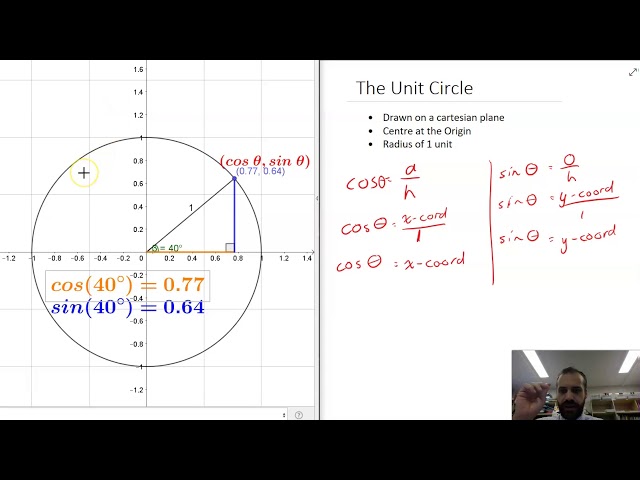
The Unit Circle
-

The Unit Circle The Tan Ratio
-

The Unit Circle and Symmetry
-

The unit circle CAST and why CAST works
-

Finding exact trig ratios involving negative angles
-

Finding exact values of trig ratios around the unit circle
-

The Unit Circle Finding exact values of negative trig ratios
-

The unit circle Boundary angles
-

The unit circle solving unknown angles
-

Solving Simple Trig Equations Worksheet (worksheet in Description)
-

The unit circle solving unknowns in trig equations
-

Sketching SinX and CosX
MA-T2: Trigonometric Functions and Identities
-

Pythagorean identity
-

Pythagorean identity rearrangement
-

Using Pythagorean Identities Part 1
-

Solving trig identity equations using quadratics
-

Solving trig identity equations using quadratics part 2
-

Solving and simplifying using trig identities
-

Sketching f(x) = tan(x) and why it looks like that.
-

Solving Trig equations The Tricky 3 Quantum of Quadratics
-

Solving Trig equations The Tricky 3 Square or Die
-

Solving Trig equations The Tricky 3 Domain Domination
-

Reciprocals of Trigonometric Functions
-

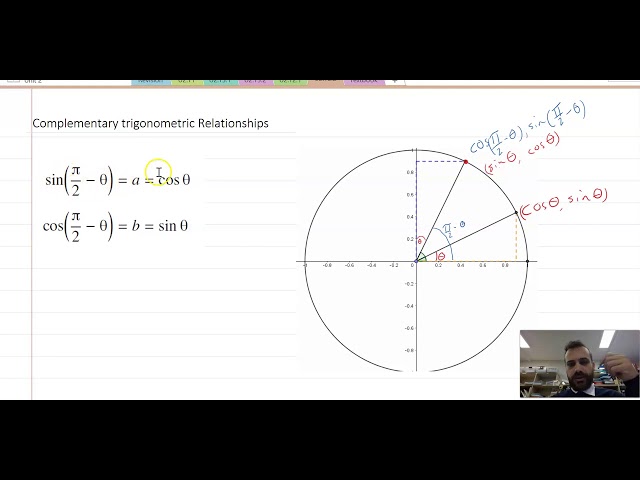
Complementary Trigonometric Relationships
-

Exact values of reciprocal trigonometric functions
-

Solving reciprocal trig functions
-

The pythagorean Identity and reciprocal trigonometric functions
-

Proving Trigonometric identities
-

2 more pythagorean identities
MA-C1: Introduction to Differentiation
-

Variable and constant rates of change
-

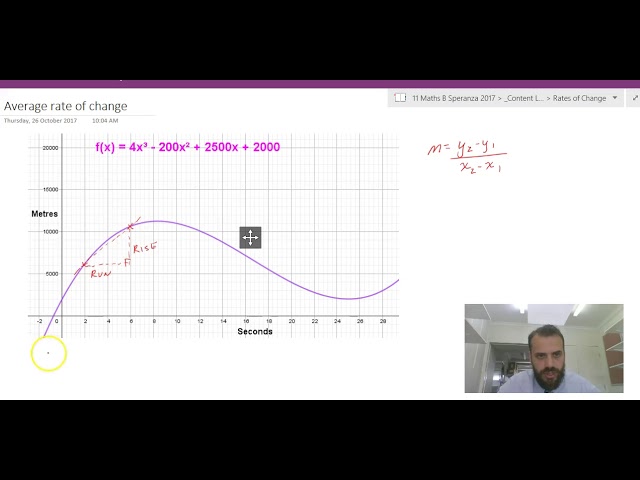
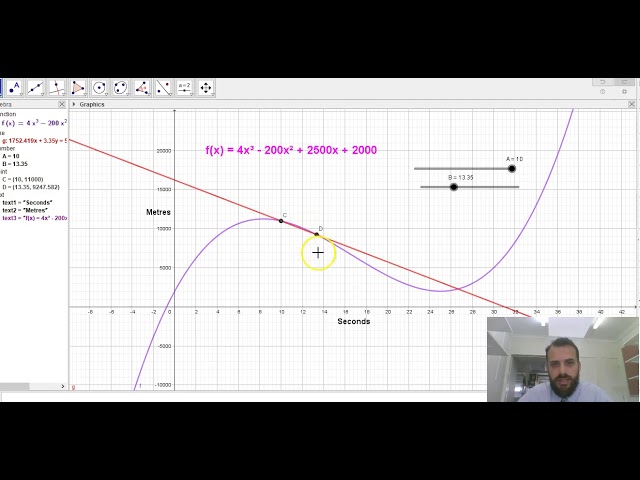
Average rates of change
-

Intro to instantaneous rates of change
-

The Gradient function
-

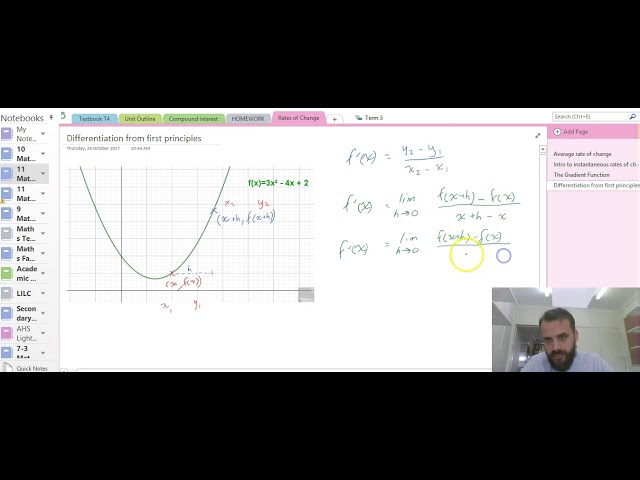
Differentiation from first principles
-

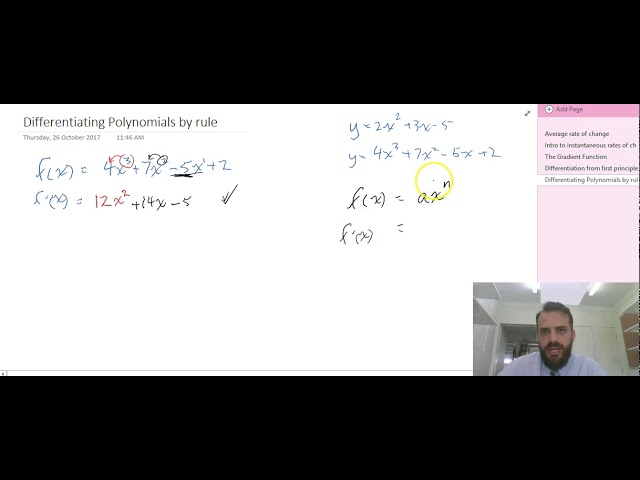
Differentiating polynomials by rule
-

Finding Stationary points
-

Nature of Stationary points
-

Optimisation when the function is unknown
-

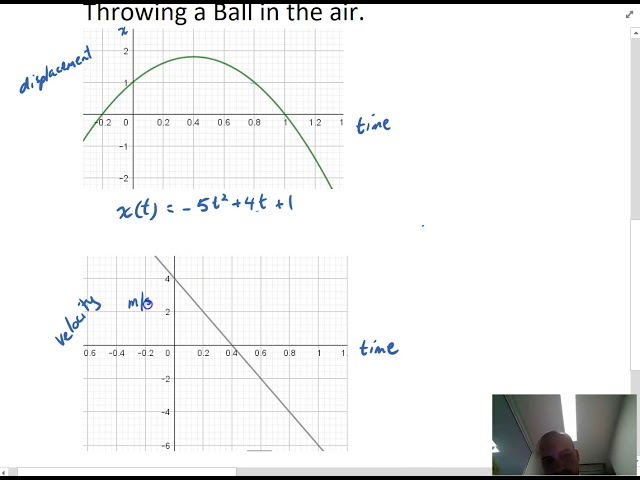
Introduction to Kinematics
-

Finding the equation of a tangent
-

Finding the equation of a normal
-

Derivatives of polynomials, negative and fractional powers by rule
-

Composite functions and the chain rule
-

The chain rule the fast way
-

The product rule
-

The quotient rule
MA-E1: Logarithms and Exponentials
-

Log laws as fast as possible
-

Logs 1 Intro to Logarithms
-

Logs 2 Log Law 1
-

Logs 3 Log Law 2
-

Logs 4 Log Law 3
-

Logs 5 Log Law 4
-

Logs 6 Log Law 5
-

Logs 7 Log Law 6
-

Logs 8 solving exponentials
-

Solving Indicial equations using logarithms
-

Logs 9 Solving logarithmic equations
-

Solving Log equations examples
-

Solving equations involving natural log
-

Solving logarithmic equations with an unknown power
-

Solving logarithmic equations with an unknown base
-

Logs 10 Solving logarithmic equations part 2
-

Logarithms 12 Simplifying Log equations
-

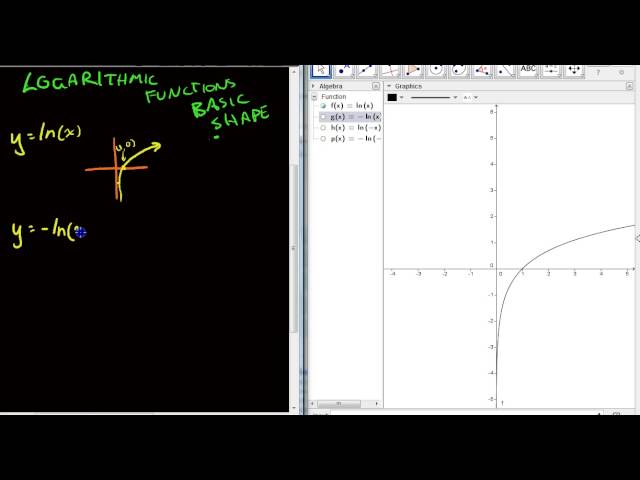
Logarithmic functions Basic shape
-

Logarithmic functions Sketching
-

Finding equations of log functions
-

Logarithmic functions 3 Find equation from a sketch
-

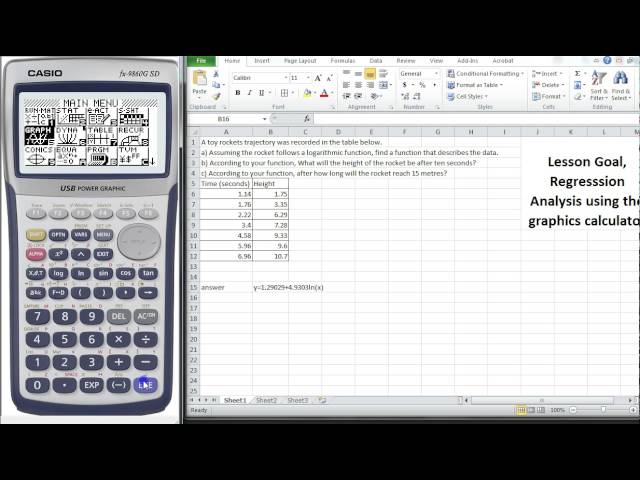
Logarithmic Functions 4 Regression analysis
-

Exponential and logarithmic modelling
-

Solving Indicial equations
-

Harder Indicial Equations
-

Indicial equations super hard quadratic action
-

Indicial equations The hardest one
-

Exponential Functions Basic shape and Translations
-

Exponential Functions Dilations
-

Exponential functions 2 Sketching
-

Exponential functions 2 Sketching
-

Exponential functions 3 Finding equation from a sketch
-

Exponential Model and Applications
-

Derivatives of Exponential, Logarithmic and Trigonmetric functions
MA-S1: Probability & Discrete Probability Distributions
S1.1: Probability and Venn diagrams
-

The Language of Sets
-

Theoretical Probability with sets
-

All Probabilities sum to 1
-

Venn Diagrams the complement
-

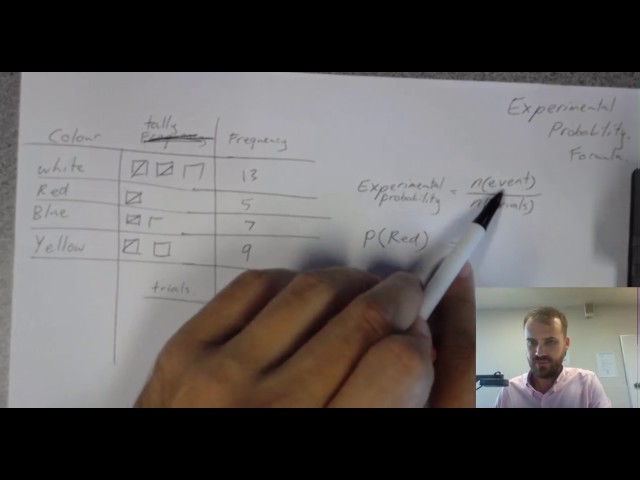
Experimental probability
-

simplified tree diagram
-

The Addition rule of probability
-

Probability Tables intro
-

Conditional Probability formula
-

Conditional Probability Do you watch the bachelorette
-

Conditional probability rearranging the formula
-

Conditional Probability and Tree Diagrams
-

Independent events intro and tests
-

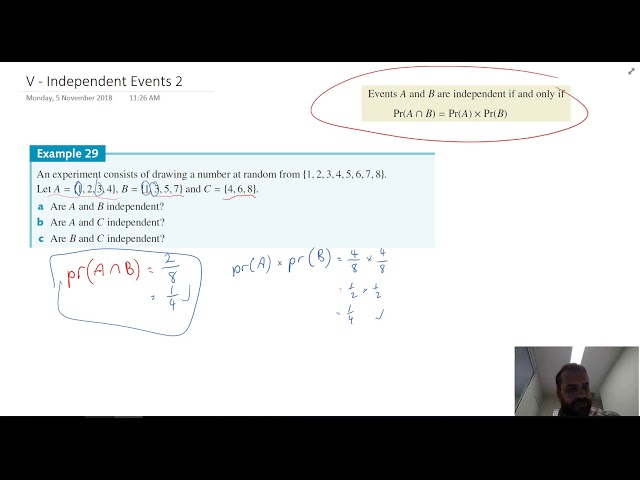
Independent events 2
-

Pascal’s Triangle and Selections
-

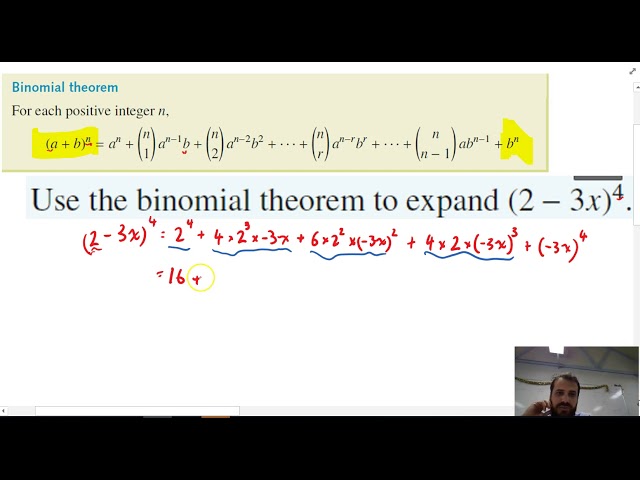
Binomial expansion using pascal’s triangle
S1.2: Discrete probability distributions
-

Discrete Random Variables: Introduction and Examples
-

Discrete Random Variables Uniform Distribution
-

Discrete Random Variable Worked Example
-

The Geometric Probability Distribution
-

Expected Value of discrete random distributions
-

Discrete random distributions Expected value challenging but important
-

Variance and Standard Deviation: Discrete Random Variables
-

Properties of Expected Value: aE(X)+b = E(aX + b)
-

The alternative Variance formula Proof
-

Alternative Variance Formula Worked Example