Unit 3
Mathematical Methods (Western Australia)
Topic 1: Functions and Graphs
-

Derivatives of exponential functions – An introduction
-

Derivatives of exponential functions Simple rules
-

Applications of derivatives of exponential Functions
-

Derivatives of periodic functions 1 A graphical explanation
-

Derivatives of Periodic functions 2 Simple examples
-

Derivatives of periodic functions Applications 1
-

Derivatives of periodic functions Applications 2
-

Derivatives of polynomials, negative and fractional powers by rule
-

Composite functions and the chain rule
-

The chain rule the fast way
-

The product rule
-

The quotient rule
-

The chain rule revisited
-

The Product Rule Revisited
-

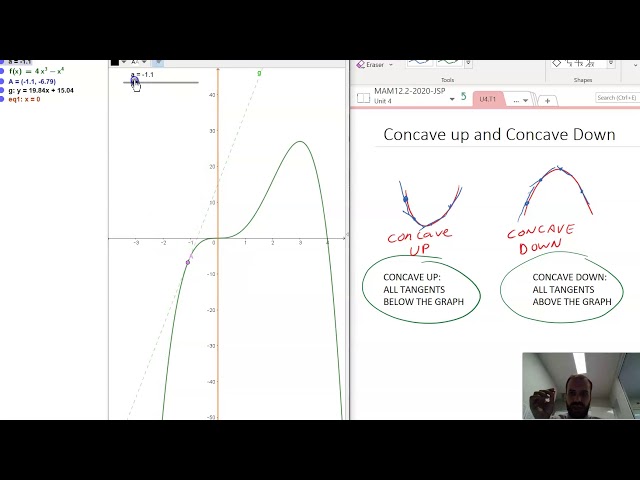
Concave up and Concave down Part 1: 2 useful definitions
-

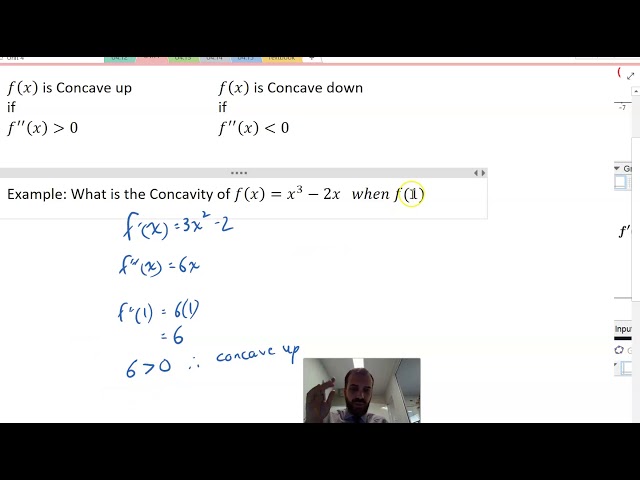
Concavity and the second derivative
-

Points of Inflection and the 2nd derivative
-

The 2nd Derivative test
-

Sketching Functions with the second derivative and Points of Inflection
-

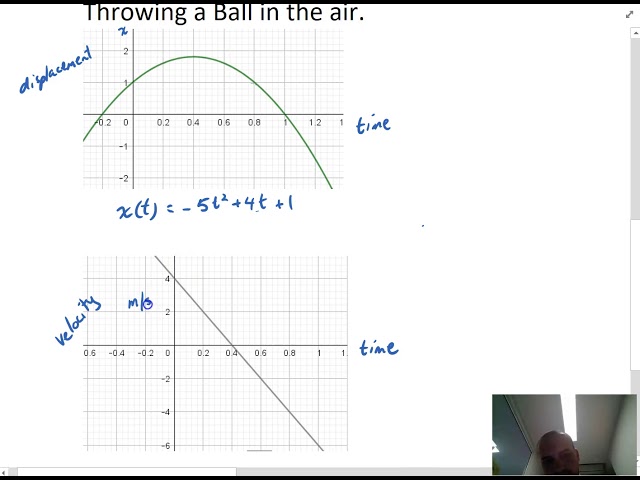
Introduction to Kinematics
-

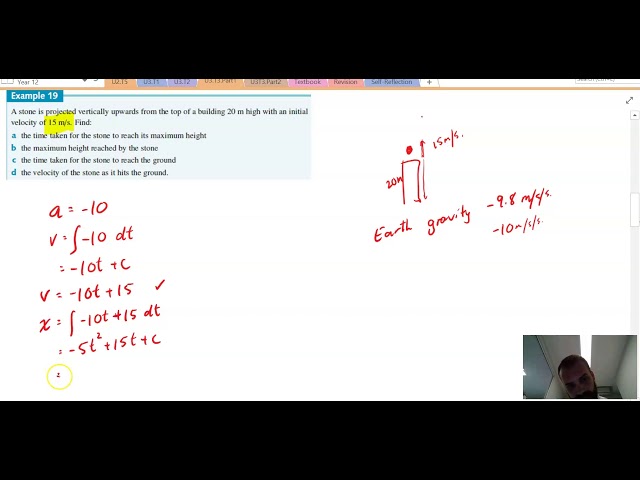
Applications of Integration in motion questions
-

Optimisation when the function is unknown
Topic 2: Integrals
-

Intro to Integration and integrating polynomials
-

Integration a little bit of theory
-

Integration finding the c value
-

Integration the reverse chain rule
-

Integration resulting in a logarithm
-

Integrals of exponentials
-

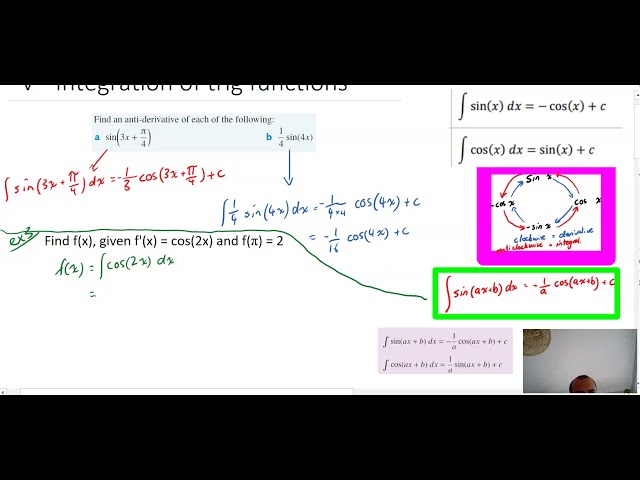
Integration of trig functions
-

Integration by recognition updated
-

Applications of Integration in motion questions
-

The definite integral
-

The definite integral signed area
-

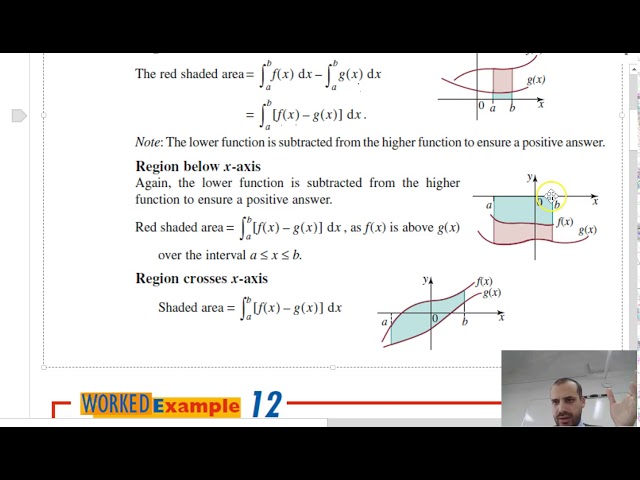
Area between two curves
-

The area under a derivative function
-

Trapezoidal Rule Fully explained
Topic 3: Discrete Random Variables
-

Discrete Random Variables
-

Discrete Random Distributions Expected value
-

Probability Distributions Discrete vs continuous random variables
-

Discrete Probability distributions 2 Properties of discrete probability distributions
-

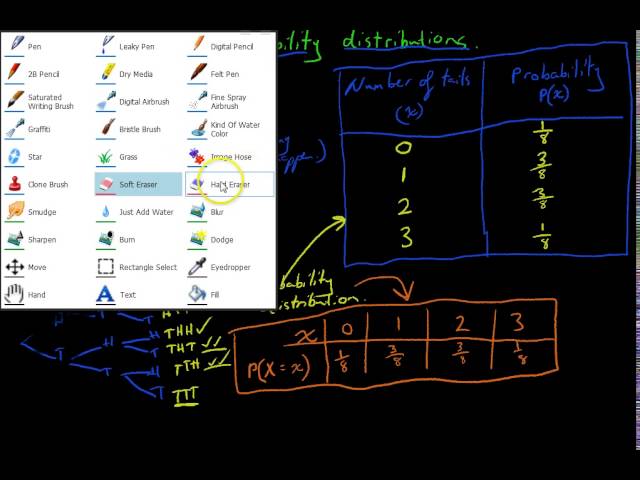
Discrete probability distribution 3 Graphing the distribution
-

Discrete probability distributions 4 Applications
-

Discrete random distributions Expected value challenging but important
-

Discrete Random Variables including conditional probability
-

how to draw Pascal’s triangle
-

Using pascals triangle to calculate combinations
-

Binomial distribution Combinations
-

Bernoulli sequence
-

Binomial distribution introduction
-

Developing Binomial Distribution Intuition
-

The binomial Probability Formula
-

Binomial Probability Distribution formula Worked Example
-

Binomial Probability formula at most and at least
-

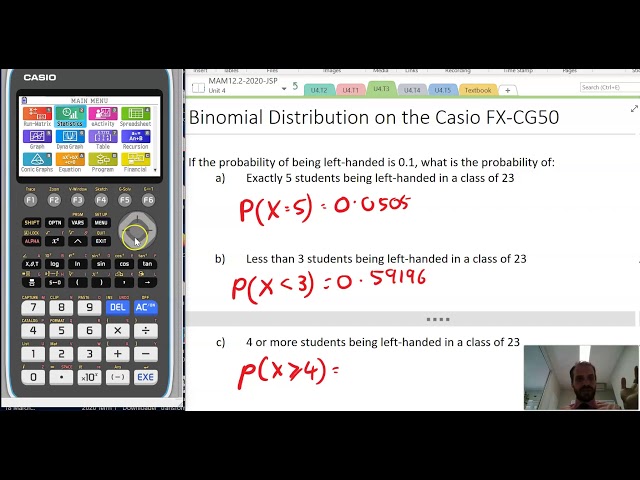
Binomial Distribution on the Casio FX CG50AU
-

Binomial Probability Conditional Probability
-

Binomial distribution expected value variance and standard deviation
-

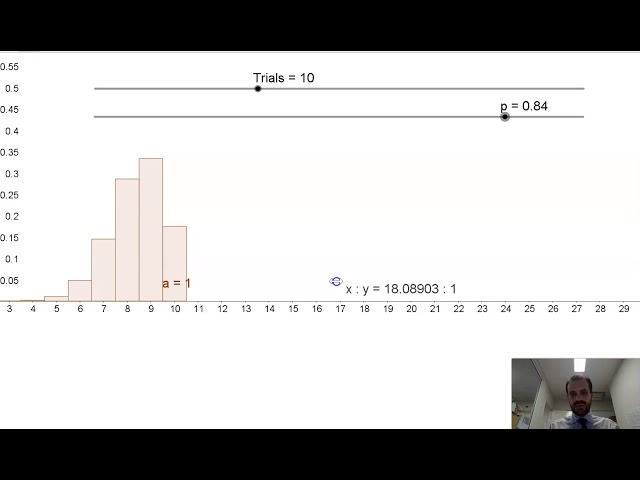
Construct a Binomial Distribution Graph
-

Binomial Distribution finding a sample size