Unit 3 & 4
Mathematical Methods (Victoria)
Differentiation & Applications
-

Derivatives of Exponential, Logarithmic and Trigonmetric functions
-

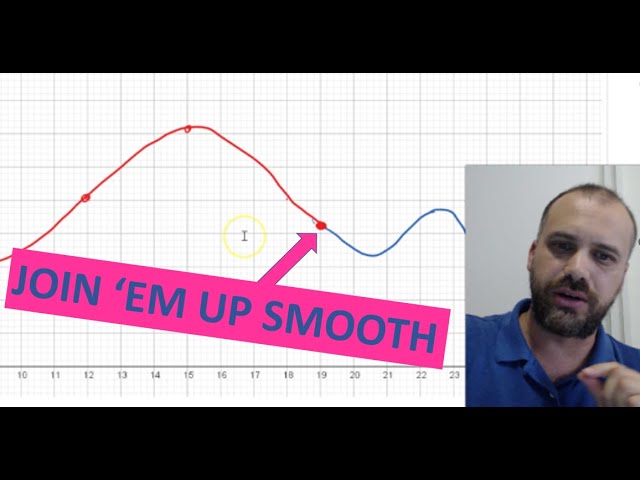
Joining two functions so that their gradients match: Part 1 (Maths Methods PSMT IA1 prep)
-

Joining two functions so that their gradients match: Part 2 (Maths Methods PSMT IA1 prep)
-

The chain rule revisited
-

The Product Rule Revisited
-

The quotient rule
-

Equations of tangents and normals revisited
-

Average vs instantaneous rates of change
-

Rates of change application
-

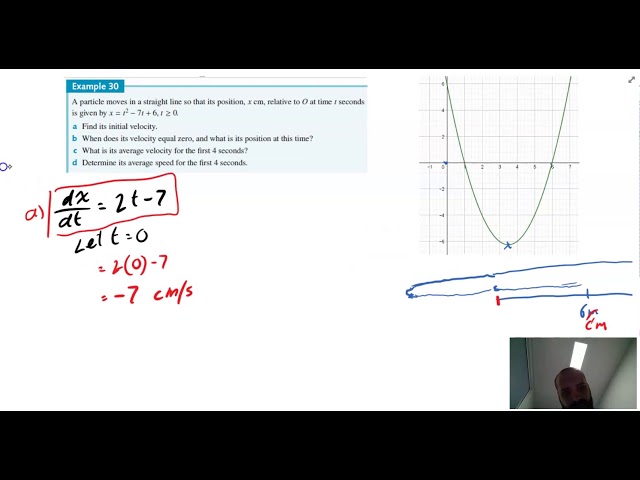
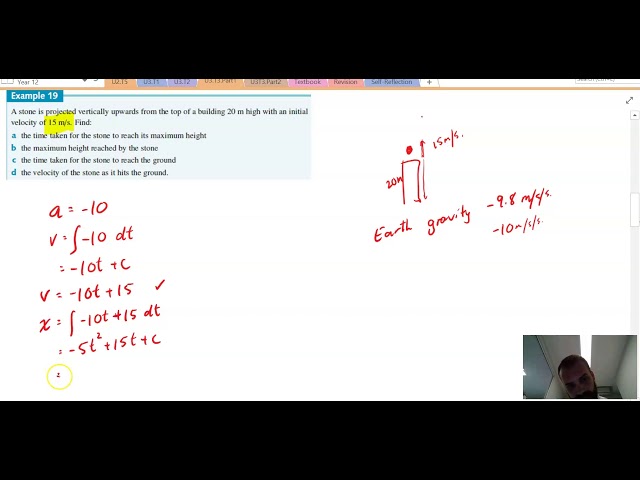
Motion in a straight line An application of rates
-

Motion in a straight line acceleration recap
-

Finding Stationary points
-

Nature of Stationary points
-

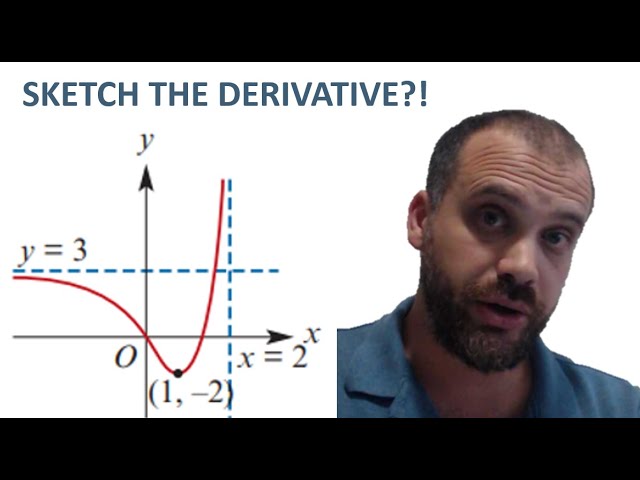
Sketching the derivative function from a picture
Integration
-

Intro to Integration and integrating polynomials
-

Integration a little bit of theory
-

Integration finding the c value
-

Integration the reverse chain rule
-

Integration resulting in a logarithm
-

Integrals of exponentials
-

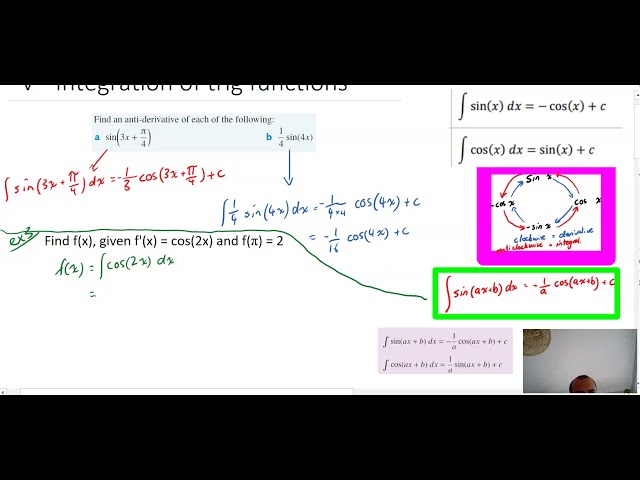
Integration of trig functions
-

Integration by recognition updated
-

Applications of Integration in motion questions
-

The definite integral
-

The definite integral signed area
-

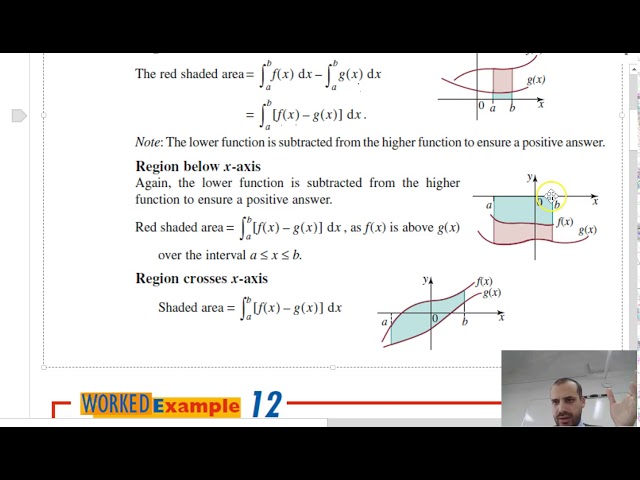
Area between two curves
-

The area under a derivative function
-

Trapezoidal Rule Fully explained
Discrete Random Variables & their Distributions
-

Discrete Random Variables
-

Discrete Random Distributions Expected value
-

Probability Distributions Discrete vs continuous random variables
-

Discrete Probability distributions 2 Properties of discrete probability distributions
-

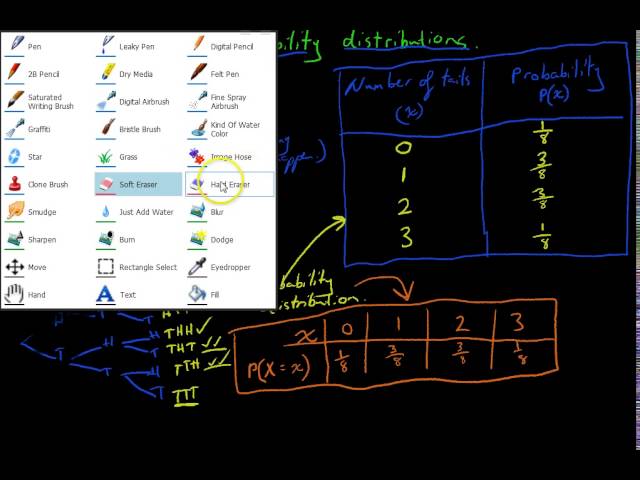
Discrete probability distribution 3 Graphing the distribution
-

Discrete probability distributions 4 Applications
-

Discrete random distributions Expected value challenging but important
-

Discrete Random Variables including conditional probability
The Binomial Distribution
-

Bernoulli sequence
-

Binomial distribution introduction
-

Developing Binomial Distribution Intuition
-

The binomial Probability Formula
-

Binomial Probability Distribution formula Worked Example
-

Binomial Probability formula at most and at least
-

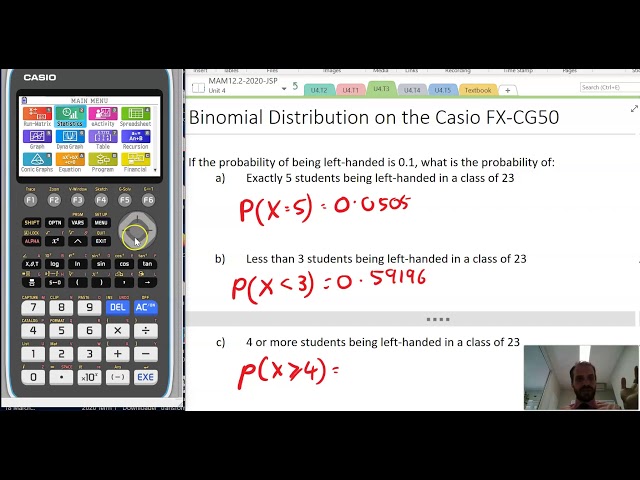
Binomial Distribution on the Casio FX CG50AU
-

Binomial Probability Conditional Probability
-

Binomial distribution expected value variance and standard deviation
-

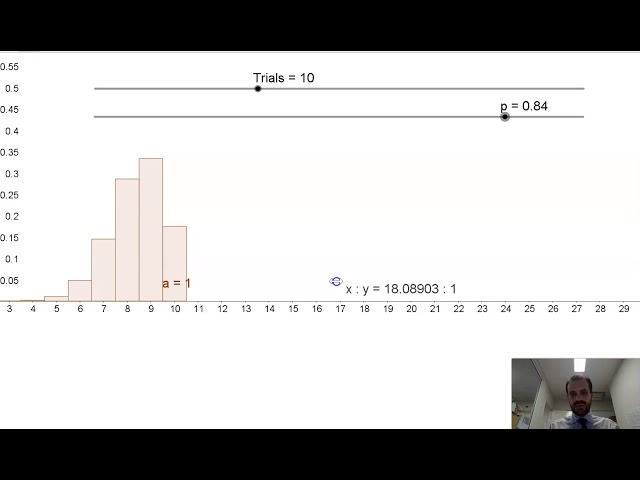
Construct a Binomial Distribution Graph
-

Binomial Distribution finding a sample size
Continuous Random Variables & The Normal Distribution
-

Estimating probability of a continuous random variable using data
-

The probability Density Function
-

Mathematical proof that you do not exist
-

Calculating probability using a probability density function
-

Proving a function is a probability density function
-

unknowns in probability density functions
-

Unbounded Probability density functions
-

The mean of a continuous random variable
-

Calculating percentiles from a probability density function
-

Calculating variance and standard deviation of a continuous random variable
-

The Cumulative Probability Distribution Function
-

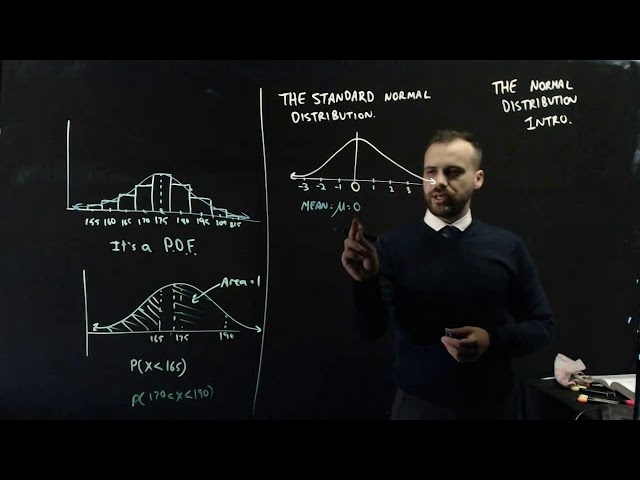
The normal distribution Introduction
-

Determining normal probabilities on the casio fx cg50AU
-

The Inverse Normal Distribution on the Casio FX CG50AU
-

The inverse normal distribution on the TI Nspire
-

A tricky normal distribution question
-

Using z scores to standardise and compare values
-

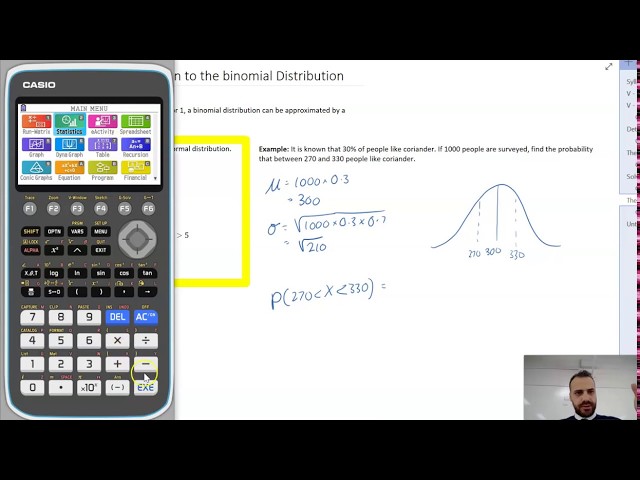
The Normal Approximation to the binomial distribution
Sampling & Estimation
-

Why is sample proportion interesting and important
-

Sampling from a small population
-

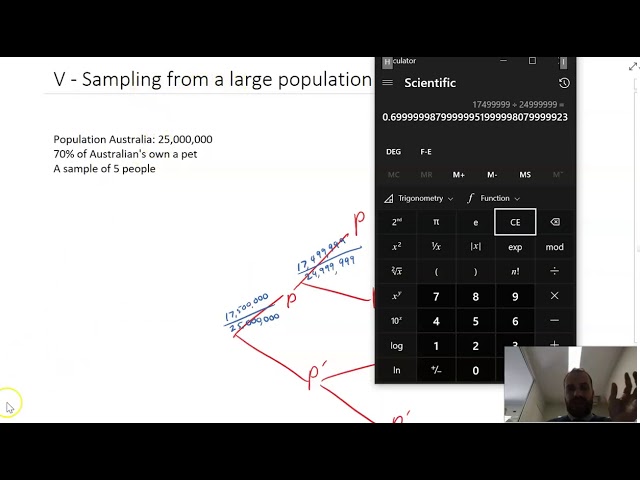
Sampling from a large population
-

Sample proportion mean and standard deviation
-

Approximating the distribution of sample proportions using the normal distribution
-

Confidence Intervals for Population proportion
-

Finding a confidence interval on the Casio FXCG50 AU Calculator
-

Determining required Sample size for a given Margin of error
-

Binomial Approximation to the normal and sample proportion, one question two ways