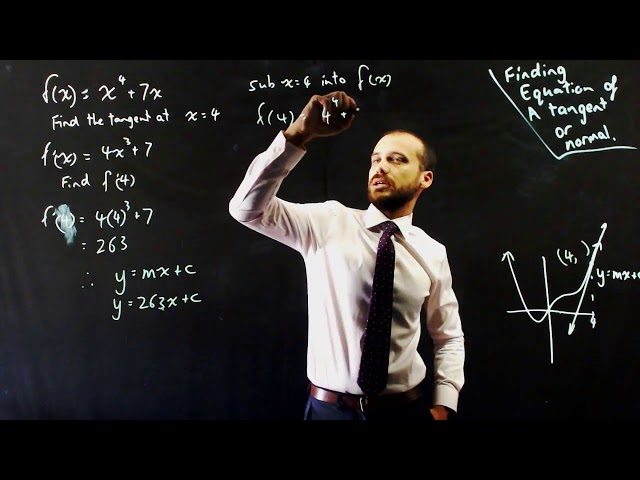Unit 2
Mathematical Methods (Queensland)
Topic 1 & 2: Exponential & Logarithmic Functions
-

Exponential Functions Basic shape and Translations
-

Exponential Functions Dilations
-

Exponential functions 2 Sketching
-

Exponential functions sketching part 2
-

Exponential functions 3 Finding equation from a sketch
-

Exponential Model and Applications
-

Logs 1 Intro to Logarithms
-

Solving Indicial equations
-

Harder Indicial Equations
-

Indicial equations super hard quadratic action
-

Indicial equations The hardest one
Topic 3: Trigonometric Functions
-

Introduction to Radians
-

Converting Radians to Degrees and Degrees to Radians
-

Radians quick angles
-

Standard triangles
-

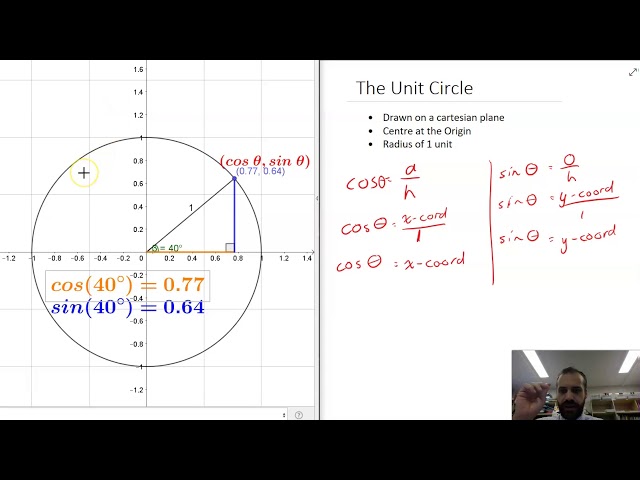
The Unit Circle
-

The Unit Circle The Tan Ratio
-

The Unit Circle and Symmetry
-

The unit circle CAST and why CAST works
-

Finding exact trig ratios involving negative angles
-

Finding exact values of trig ratios around the unit circle
-

The Unit Circle Finding exact values of negative trig ratios
-

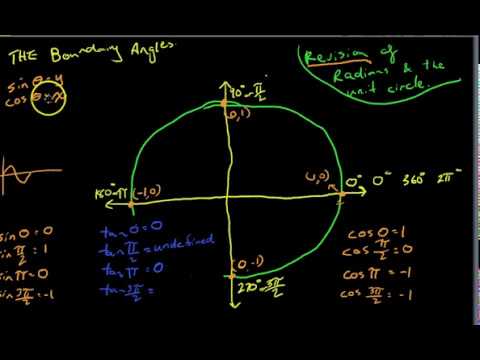
The unit circle Boundary angles
-

The unit circle solving unknown angles
-

Solving Simple Trig Equations Worksheet (worksheet in Description)
-

The unit circle solving unknowns in trig equations
-

Pythagorean identity
-

Pythagorean identity rearrangement
-

Using Pythagorean Identities Part 1
-

Solving trig identity equations using quadratics
-

Solving trig identity equations using quadratics part 2
-

Sketching SinX and CosX
-

Sketching y = AsinX and AcosX
-

Sketching y = AsinX +D and AcosX + D
-

Sketching y = AsinBx + D or y = AcosBx +D
-

Sketching y = AsinB(x+C)+D
-

Finding the equation of a periodic function from a graph or sketch
-

Revision of radians and the unit circle
-

Solving and simplifying using trig identities
-

Solving Trig equations The Tricky 3 Quantum of Quadratics
-

Solving Trig equations The Tricky 3 Square or Die
-

Solving Trig equations The Tricky 3 Domain Domination
-

Sketching f(x) = tan(x) and why it looks like that.
Topic 4: Introduction to Differential Calculus
-

Variable and constant rates of change
-

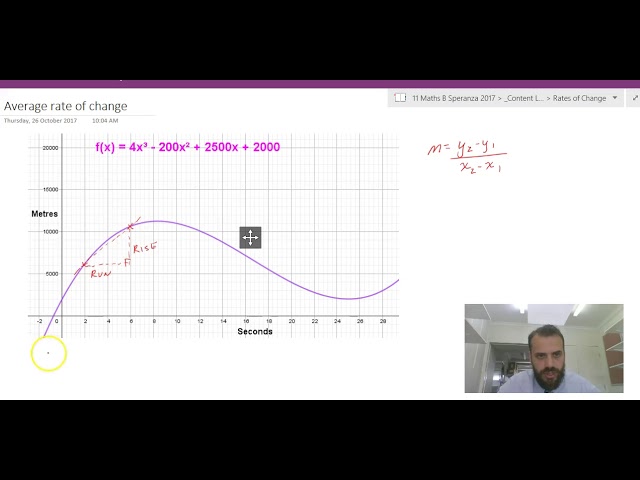
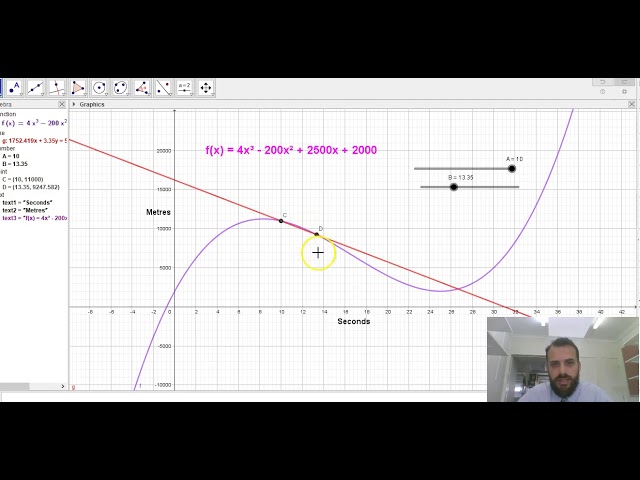
Average rates of change
-

Intro to instantaneous rates of change
-

The Gradient function
-

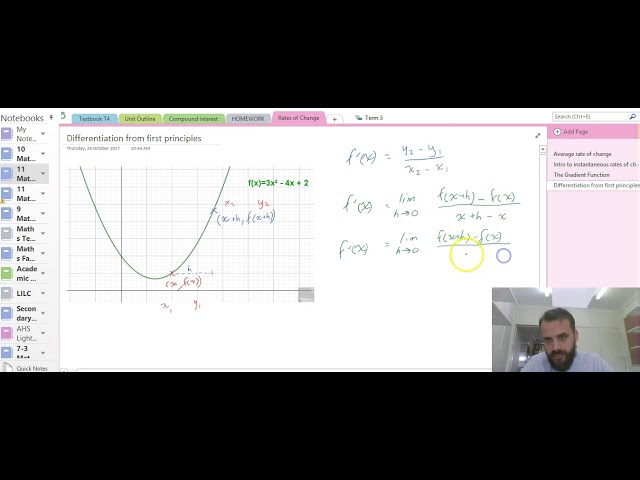
Differentiation from first principles
-

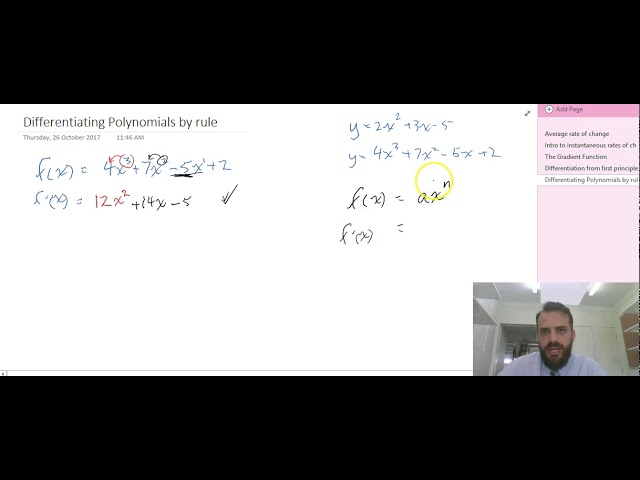
Differentiating polynomials by rule
-

Finding Stationary points
-

Nature of Stationary points
-

Optimisation when the function is unknown
-

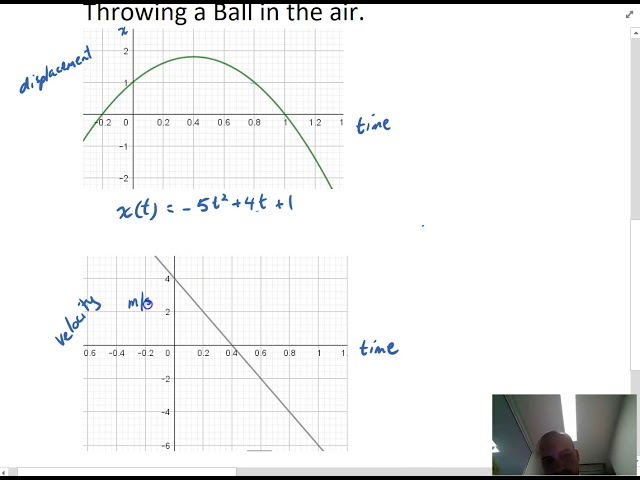
Introduction to Kinematics
-

Finding the equation of a tangent
-

Finding the equation of a normal
Topic 5: Further Differentiation and Applications 1
Topic 6: Discrete Random Variables 1
-

Discrete Random Variables: Introduction and Examples
-

Discrete Random Variables Uniform Distribution
-

Discrete Random Variable Worked Example
-

The Geometric Probability Distribution
-

Expected Value of discrete random distributions
-

Discrete random distributions Expected value challenging but important
-

Variance and Standard Deviation: Discrete Random Variables
-

Properties of Expected Value: aE(X)+b = E(aX + b)
-

The alternative Variance formula Proof
-

Alternative Variance Formula Worked Example