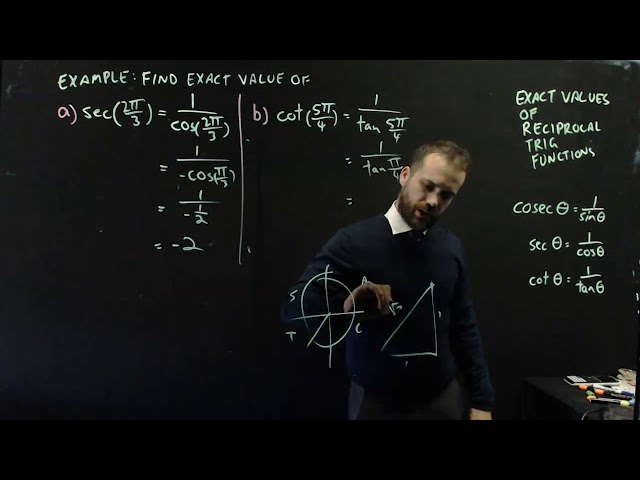Unit 2
Specialist Mathematics (Queensland)
Topic 1 & 2: Complex Numbers
-

Introduction to imaginary and complex numbers
-

Working with imaginary and complex numbers
-

Raising i to a power
-

Simplifying with powers of i
-

Adding and subtracting complex numbers
-

Multiplying complex numbers by a constant
-

Multiply complex numbers
-

Equality of complex numbers
-

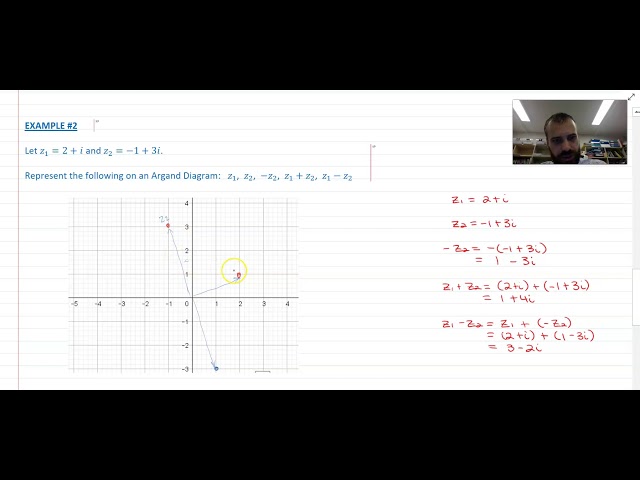
Conjugates definition and the argand diagram
-

Multiplying conjugates of complex numbers
-

Dividing complex numbers using conjugates
-

Solving equations over C
-

Completing the square with complex numbers
-

Argand Diagrams What complex numbers and Vectors have in common
-

Complex Numbers in Polar form
-

Multiplying and dividing complex numbers
-

De Moivre’s Theorem for raising a complex number to a power
-

Sketching Subsets of the complex Plane
Topic 3: Circle and Geometric Proofs
-

Geometric proofs from the ground up
-

Proving the angle in a semi-circle is a right angle
-

Prove the angle at the centre theorem
-

The angle on the same arc theorem
-

Alternate Segment Theorem Proof
-

Proving Tangent to a circle and the radius are perpendicular Using Proof by Contradiction
-

Geometric Proofs using Vectors part 1
-

Geometric proofs using vectors Part 2
Topic 4: Trigonometry and functions
-

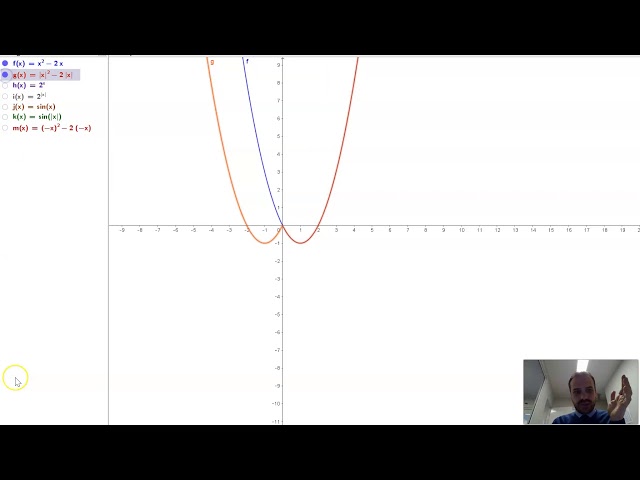
The modulus or absolute value function introduction
-

The modulus or absolute value solving equations
-

Solving Absolute value: quadratic equations
-

Absolute Value Functions
-

Sketch Absolute Value Functions with a vertical shift
-

Sketching an absolute value function worked example
-

Reflecting Functions in the y axis using absolute value functions
-

Reciprocals of functions
-

Sketching Reciprocal Functions Worked Example
-

Reciprocals of Trigonometric Functions
-

Transformations of the reciprocal Trigonometric functions
-

Sketching Tan Functions
-

Exact values of reciprocal trigonometric functions
-

Solving reciprocal trig functions
-

Pythagorean identity
-

Pythagorean identity rearrangement
-

Using the Pythagorean Identity Part 1
-

The pythagorean Identity and reciprocal trigonometric functions
-

Proving Trigonometric identities
-

2 more pythagorean identities
-

Angle sum and difference indentities
-

Angle sum and difference identities part 2
-

Double angle identity proofs and an example
-

More proofs of trig identities
-

Express the sum of trigonometric functions as a single function
-

Express the sum of trigonometric functions as a single function part 2
-

Product Sum Trigonometric Identities
Topic 5: Matrices and transformations
-

Linear Transformations Translations
-

Linear Transformations Dilations
-

Linear Transformations Dilations Part 2
-

Linear Transformations Rotations
-

Linear Transformations Reflections in the line y =mx
-

Linear Transformations Reflections with double angle identities
-

Composition of Matrices
-

Linear Transformations Inverses
-

Linear Transformations Determinants and Area