Unit 3
Mathematical Methods (Queensland)
Topic 1: Differentiation of exponential and logarithmic functions
-

Derivatives of exponential functions – An introduction
-

Derivatives of exponential functions Simple rules
-

Applications of derivatives of exponential Functions
-

Derivatives of Exponential, Logarithmic and Trigonmetric functions
-

Exponential Models using e
-

Solving equations involving natural log
-

e to the power of ln(x)
-

Derivatives of logarithmic functions Introduction
-

Derivatives of Logarithmic Functions – Simple rules
-

Logarithmic Modelling 3 Quick Examples
Topic 2: Differentiation of trigonometric functions and differentiation rules
Topic 3: Further applications of differentiation
-

Joining two functions so that their gradients match: Part 1 (Maths Methods PSMT IA1 prep)
-

Joining two functions so that their gradients match: Part 2 (Maths Methods PSMT IA1 prep)
-

Average vs instantaneous rates of change
-

Rates of change application
-

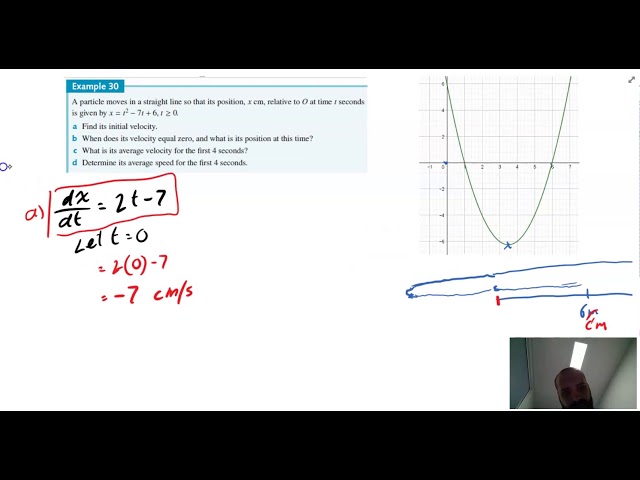
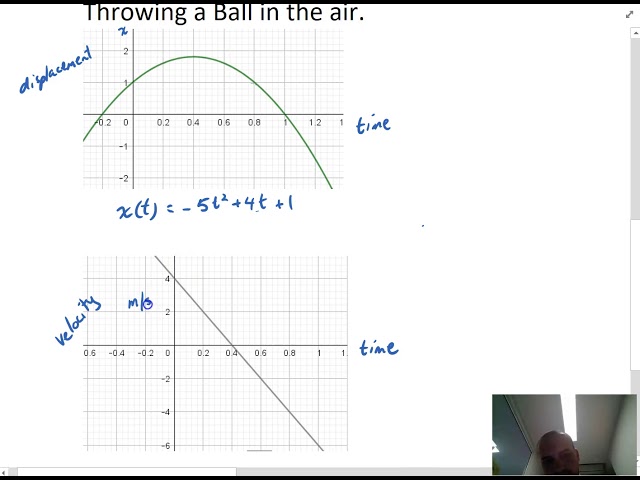
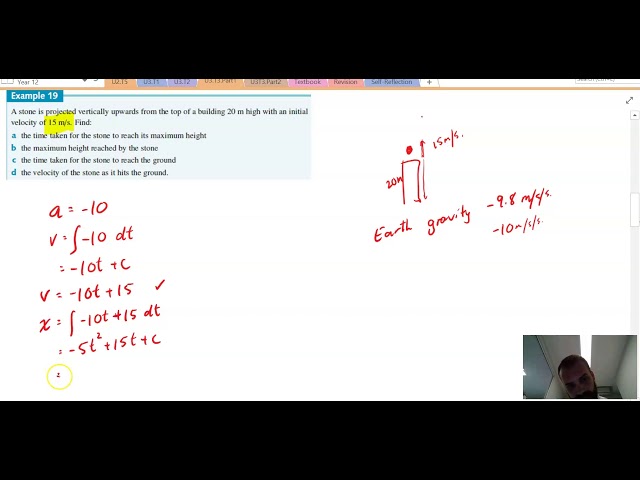
Motion in a straight line An application of rates
-

Motion in a straight line acceleration recap
-

Finding Stationary points
-

Nature of Stationary points
-

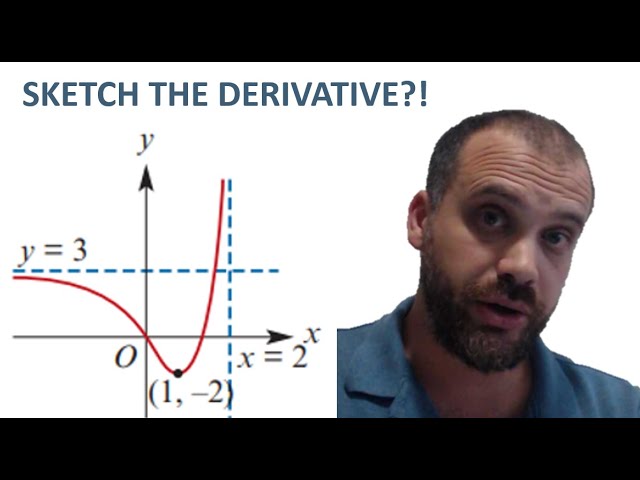
Sketching the derivative function from a picture
-

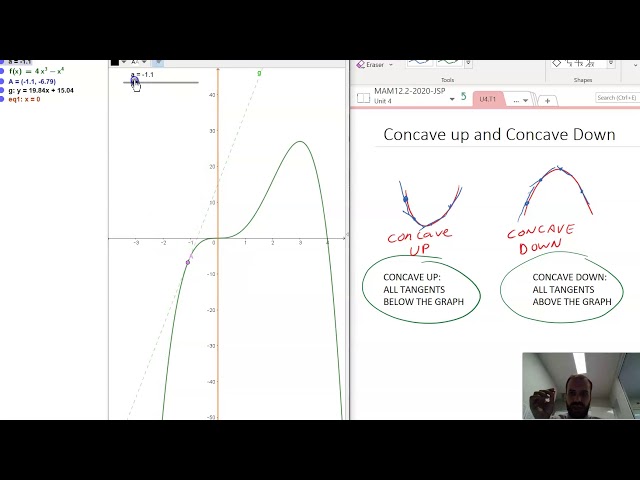
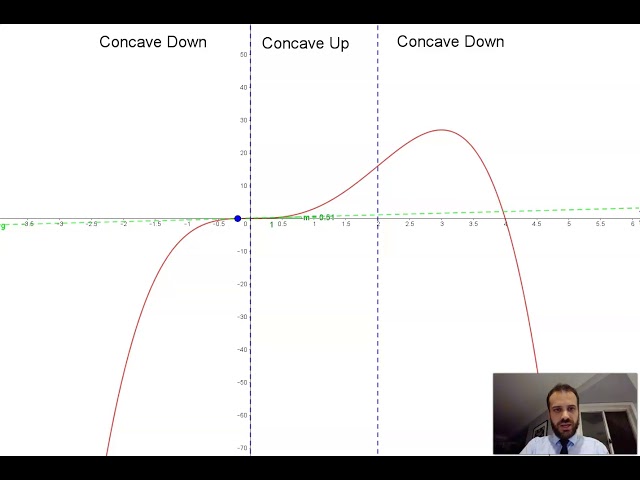
Concave up and Concave down Part 1: 2 useful definitions
-

Concave up and Concave Down Part 2 A more useful definition
-

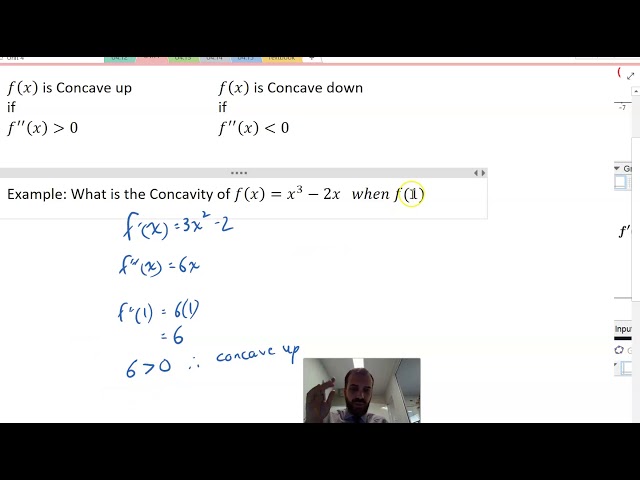
Concavity and the second derivative
-

Points of Inflection and the 2nd derivative
-

The 2nd Derivative test
-

Sketching Functions with the second derivative and Points of Inflection
-

Introduction to Kinematics
-

Optimisation when the function is unknown
-

A fun Optimisation Question
-

Optimisation: Optimising Profit
Topic 4: Introduction to integration
-

Intro to Integration and integrating polynomials
-

Integration a little bit of theory
-

Integration finding the c value
-

Integration the reverse chain rule
-

Integration resulting in a logarithm
-

integration integral of exponentials
-

Integration by recognition updated
-

Applications of Integration in motion questions
Topic 5: Discrete random variables
-

Discrete Random Variables: Introduction and Examples
-

Discrete Random Variables Uniform Distribution
-

Discrete Random Variable Worked Example
-

The Geometric Probability Distribution
-

Expected Value of discrete random distributions
-

Discrete random distributions Expected value challenging but important
-

Variance and Standard Deviation: Discrete Random Variables
-

Properties of Expected Value: aE(X)+b = E(aX + b)
-

The alternative Variance formula Proof
-

Alternative Variance Formula Worked Example
-

Bernoulli sequence
-

Binomial distribution introduction
-

Developing Binomial Distribution Intuition
-

The binomial Probability Formula
-

Binomial Probability Distribution formula Worked Example
-

Binomial Probability formula at most and at least
-

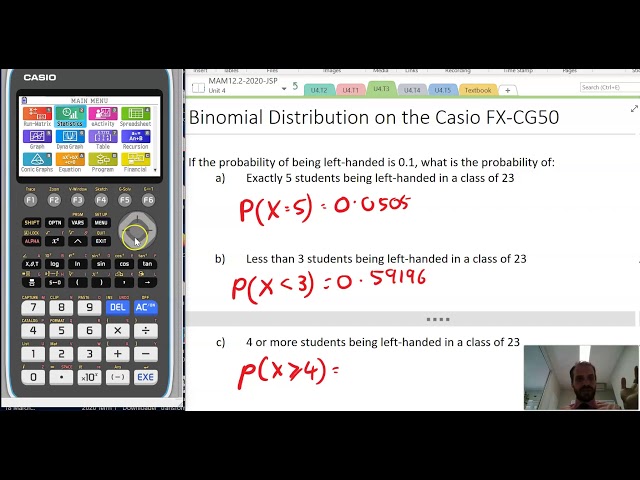
Binomial Distribution on the Casio FX CG50AU
-

Binomial Probability Conditional Probability
-

Binomial distribution expected value variance and standard deviation
-

Construct a Binomial Distribution Graph
-

Binomial Distribution finding a sample size
-

Binomial Probability: What Happens If We All Guess Every Multiple Choice Question? Maths Methods