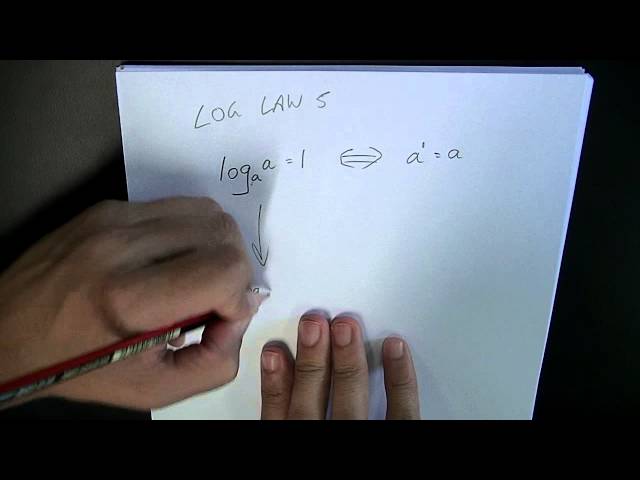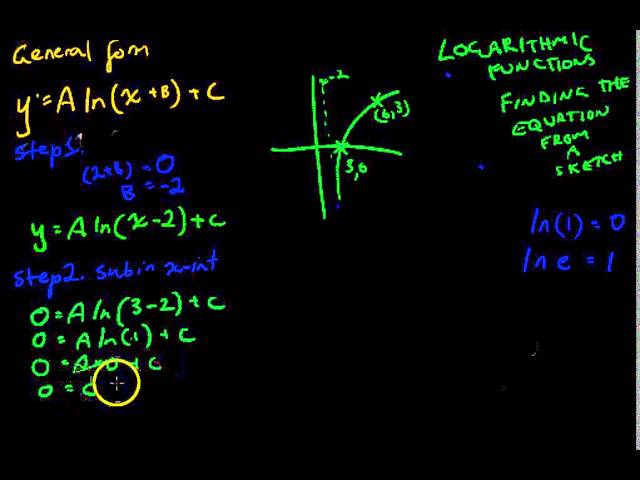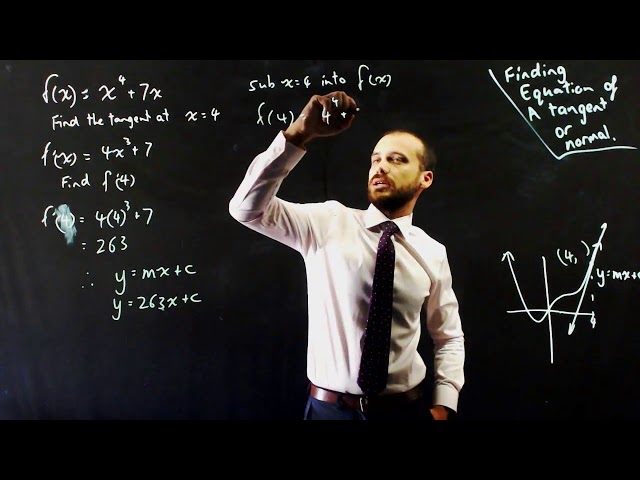Unit 2
Mathematical Methods (Queensland)
Topic 1: Exponential functions
-

Index Law 1 – multiplication of indices
-

Index Law 2 – dividing indices
-

Index Law 3 – raising to the power of zero
-

Index Law 4 – Raising a power to another power
-

Index Law 5 – worked examples using the fifth index law
-

Index Law 6 – expanding brackets around a fraction raised to a power
-

Index law 7 Negative Indices – converting Negative indices into positive indices using fractions
-

Index Laws Fractional indices
-

Index Laws Negative bases
-

Index Laws simplifying by decomposing
-

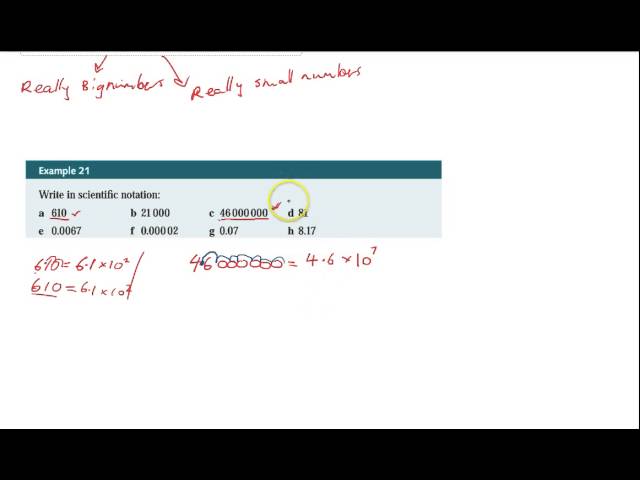
Scientific notation Converting to scientific notation
-

Scientific Notation Convert scientific notation to decimal
-

Scientific notation Multiplying and dividing
-

Exponential Functions Basic shape and Translations
-

Exponential Functions Dilations
-

Exponential functions 2 Sketching
-

Exponential functions sketching part 2
-

Exponential functions 3 Finding equation from a sketch
-

Exponential Model and Applications
-

Solving Indicial equations
-

Harder Indicial Equations
-

Indicial equations super hard quadratic action
-

Indicial equations The hardest one
Topic 2: Logarithms and logarithmic functions
-

Log laws as fast as possible
-

Logs 1 Intro to Logarithms
-

Logs 2 Log Law 1
-

Logs 3 Log Law 2
-

Logs 4 Log Law 3
-

Logs 5 Log Law 4
-

Logs 6 Log Law 5
-

Logs 7 Log Law 6
-

Logs 8 solving exponentials
-

Logs 9 Solving logarithmic equations
-

Solving Indicial equations using logarithms
-

Solving Log equations examples
-

Solving logarithmic equations with an unknown power
-

Solving logarithmic equations with an unknown base
-

Logs 10 Solving logarithmic equations part 2
-

Logarithms 12 Simplifying Log equations
-

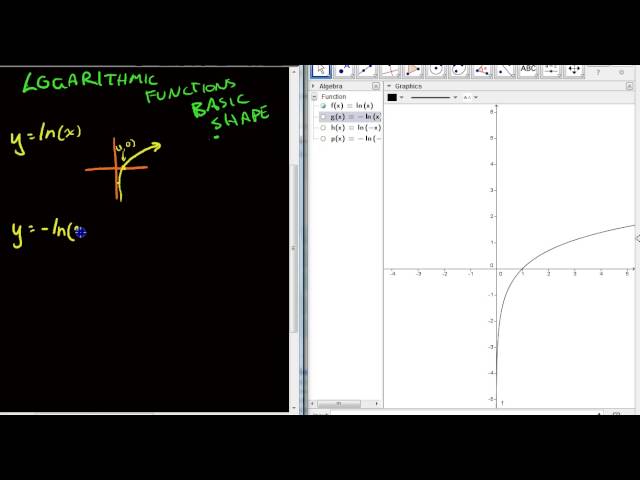
Logarithmic functions Basic shape
-

Logarithmic functions Sketching
-

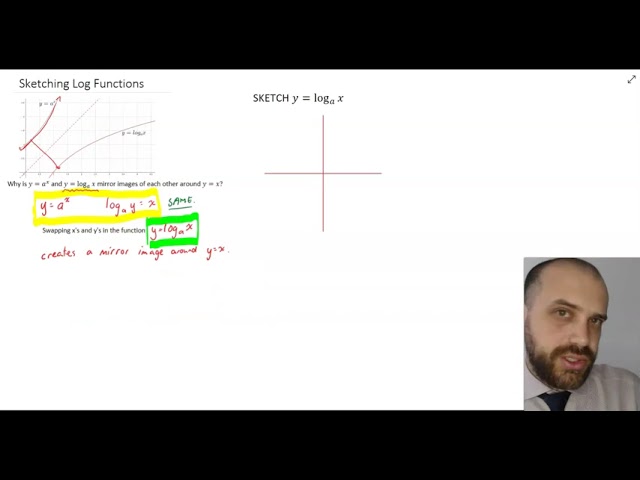
Sketching Log Functions & why they look the way they do
-

Finding equations of log functions
-

Logarithmic functions 3 Find equation from a sketch
-

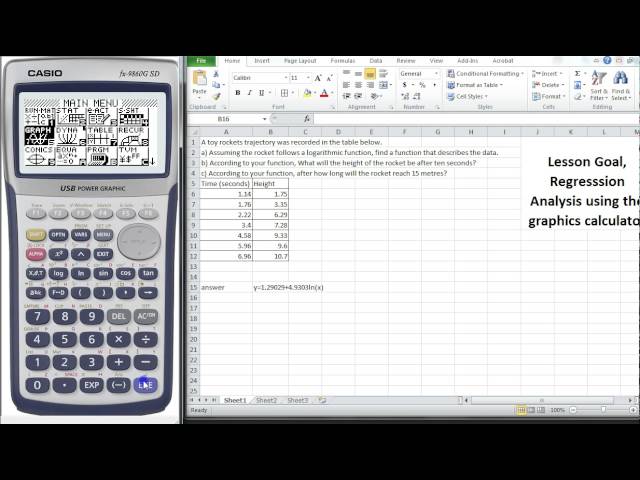
Logarithmic Functions 4 Regression analysis
-

Exponential and logarithmic modelling
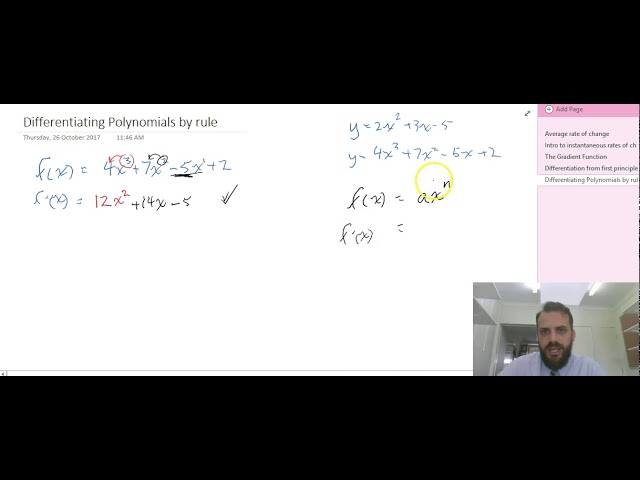
Topic 3: Introduction to differential calculus
Topic 4: Applications of differential calculus
-

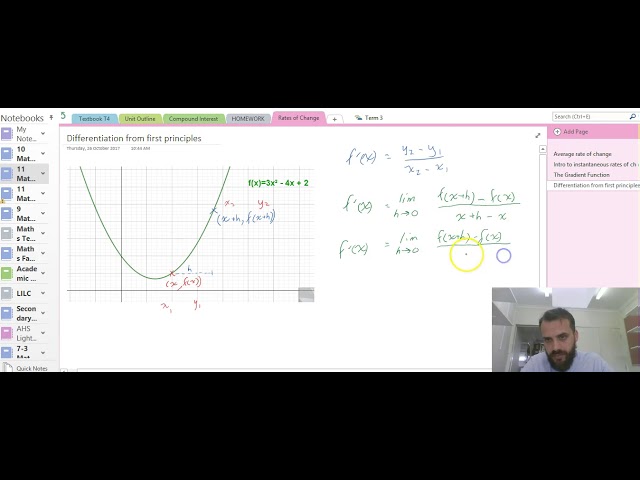
Intro to instantaneous rates of change
-

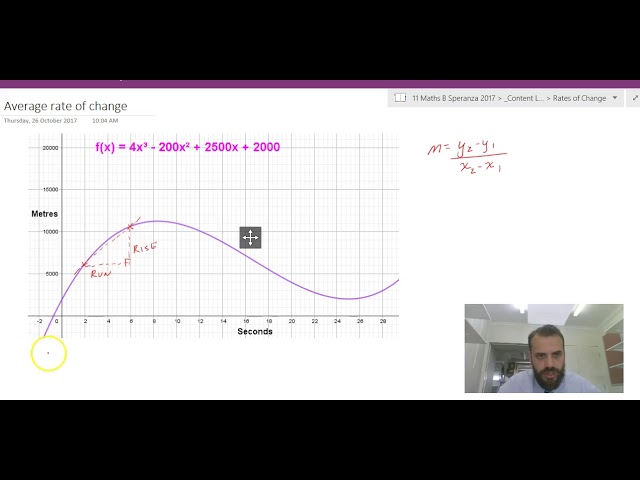
Average vs instantaneous rates of change
-

Finding the instantaneous rate of change
-

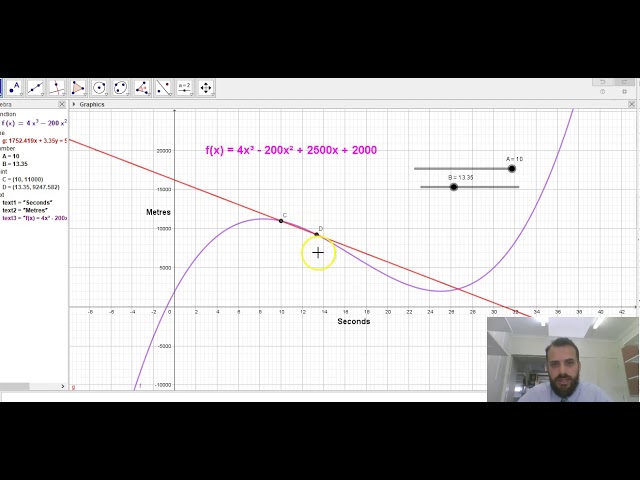
Finding the equation of a tangent
-

Finding the equation of a normal
-

Equations of tangents and normals revisited
-

Finding Stationary points
-

Nature of Stationary points
-

Finding the nature of turning points
-

Interpreting displacement time graphs
-

Interpreting velocity time graphs
-

Differentiation and displacement velocity and acceleration