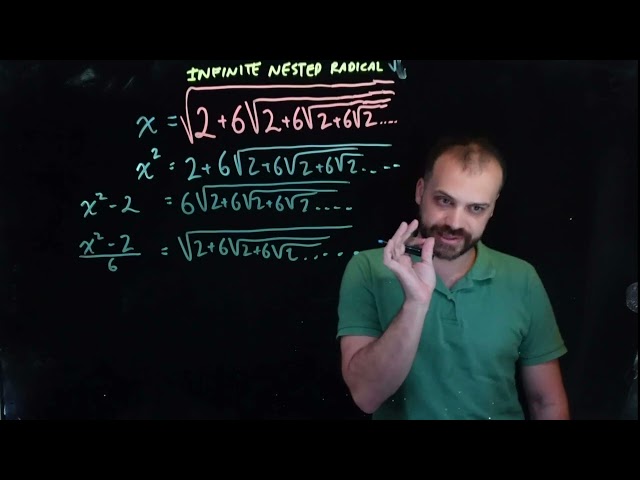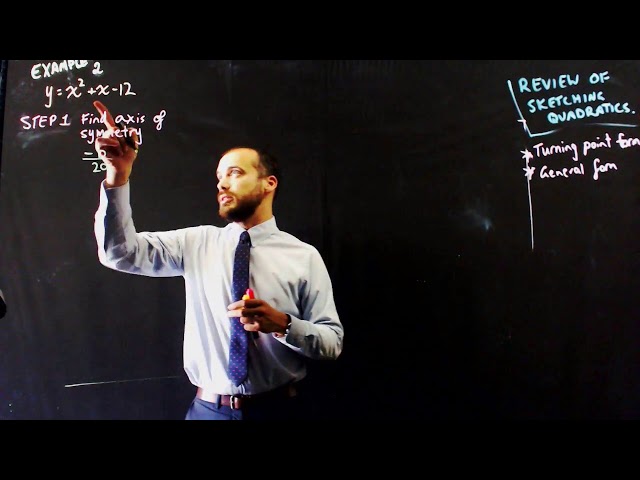Unit 1
Mathematical Methods (Queensland)
Topic 1: Surds and quadratic functions
-

Surds: What they are and why we need them
-

Proof that the square root is equal to the power of 1/2
-

Simplifying surds
-

Adding and Subtracting surds by grouping like terms
-

Multiplying surds
-

Surds and the distributive law
-

Dividing Surds
-

Surds Rationalising denominators
-

Rationalising denominators using conjugates
-

Infinite nested radicals
-

Anatomy of a quadratic graph
-

Solving Quadratics 3 ways
-

3 forms of the quadratic equation
-

Review of sketching quadratics two ways
-

The quadratic formula and the discriminant
-

Modelling and problem solving with quadratics
-

solving simultaneous equations using quadratic and linear graphs
Topic 2: Binomial expansion and cubic functions
-

Pascal’s Triangle and Selections
-

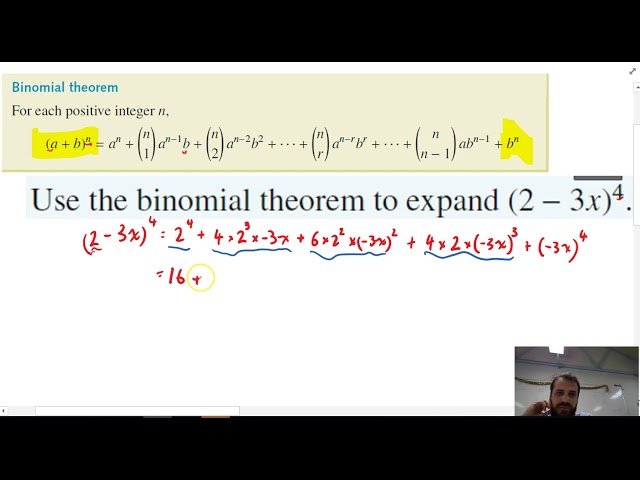
Binomial expansion using pascal’s triangle
-

Finding a linear factor of a polynomial
-

Factorise solve and sketch a cubic
-

Cubics in “Turning Point” Form: (But it’s not a turning point)
-

Graphing and finding key points on the TI Nspire
-

Determining intersections of functions graphically on the TI Nspire
-

Sketching a graph on the TI Nspire
-

Solving simultaneous equations using LinSolve TI Nspire
-

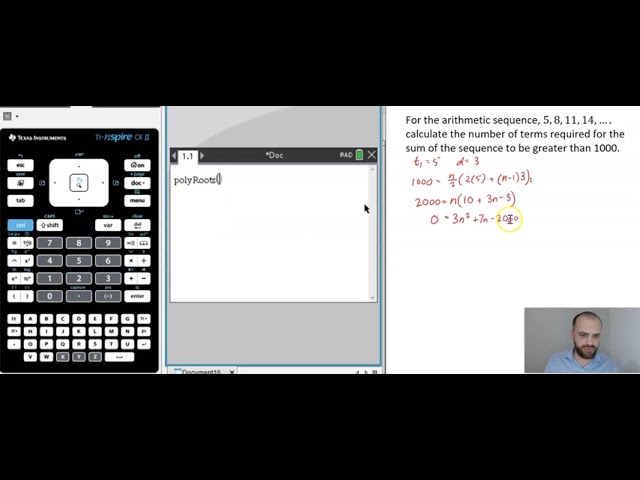
Solving polynomials on the TI Nspire
Topic 3: Functions and relations
-

Set Notation: Introduction
-

Interval Notation and Number Lines
-

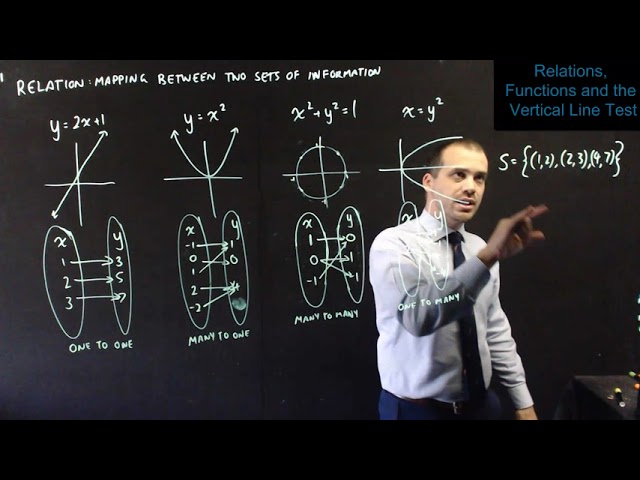
Relations Domain and Range
-

Relations, Functions and the vertical line test
-

domain and range notation
-

Domain and Range of functions and relations
-

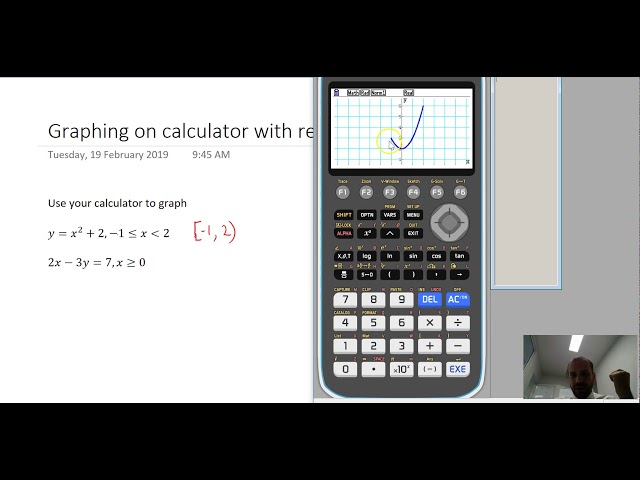
Graphing on calculator using restricted domains
-

What’s a function
-

Function notation
-

Function Notation: Better ways of representing functions
-

Piecewise Functions
-

Function Transformations intro
-

Functions Transformation fx+a
-

Function transformation f(x+a)
-

Function transformation afx
-

Functions transformations f(ax)
-

Direct vs inverse proportion
-

Equations of hyperbola and sketching
-

Finding equation of reciprocal function from sketch
-

Sketching Hyperbolas and why there’s an asymptote
-

Sketching circles and finding equations of circles
-

The square root function
-

Intersecting Functions
Topic 4: Trigonometric functions
-

Introduction to Radians
-

Converting Radians to Degrees and Degrees to Radians
-

Radians quick angles
-

Standard triangles
-

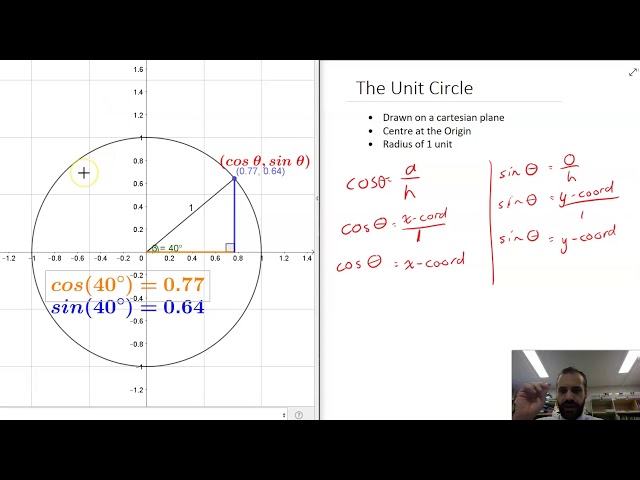
The Unit Circle
-

The Unit Circle The Tan Ratio
-

The Unit Circle and Symmetry
-

The unit circle CAST and why CAST works
-

Finding exact values of trig ratios around the unit circle
-

The Unit Circle Finding exact values of negative trig ratios
-

Finding exact trig ratios involving negative angles
-

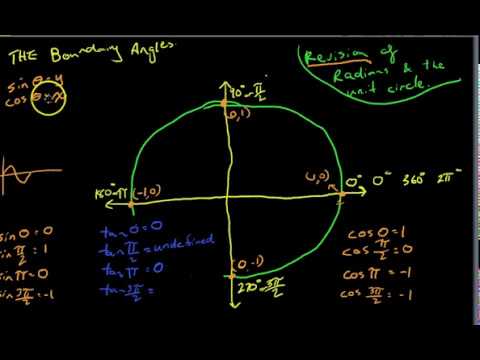
The unit circle Boundary angles
-

The unit circle solving unknown angles
-

Solving Simple Trig Equations Worksheet (worksheet in Description)
-

The unit circle solving unknowns in trig equations
-

Pythagorean identity
-

Pythagorean identity rearrangement
-

Using Pythagorean Identities Part 1
-

Solving trig identity equations using quadratics
-

Solving trig identity equations using quadratics part 2
-

Sketching SinX and CosX
-

Sketching y = AsinX and AcosX
-

Sketching y = AsinX +D and AcosX + D
-

Sketching y = AsinBx + D or y = AcosBx +D
-

Sketching y = AsinB(x+C)+D
-

Finding the equation of a periodic function from a graph or sketch
-

Revision of radians and the unit circle
-

Solving and simplifying using trig identities
-

Solving Trig equations The Tricky 3 Quantum of Quadratics
-

Solving Trig equations The Tricky 3 Square or Die
-

Solving Trig equations The Tricky 3 Domain Domination
-

Sketching f(x) = tan(x) and why it looks like that.
Topic 5: Probability
-

The Language of Sets
-

Theoretical Probability with sets
-

All Probabilities sum to 1
-

Venn Diagrams Intro
-

Venn Diagrams simple Probabilities
-

Venn Diagrams the complement
-

Venn Diagrams the intersection
-

Venn Diagrams The union
-

Venn Diagrams: Calculating Probabilities including intersections, unions and complements
-

Experimental probability
-

simplified tree diagram
-

The Addition rule of probability
-

Probability Tables intro
-

Probability with two way tables
-

Two way tables and conditional probability
-

Conditional Probability formula
-

Conditional Probability Do you watch the bachelorette
-

Conditional probability rearranging the formula
-

Conditional Probability and Tree Diagrams
-

Independent events intro and tests
-

Independent events 2