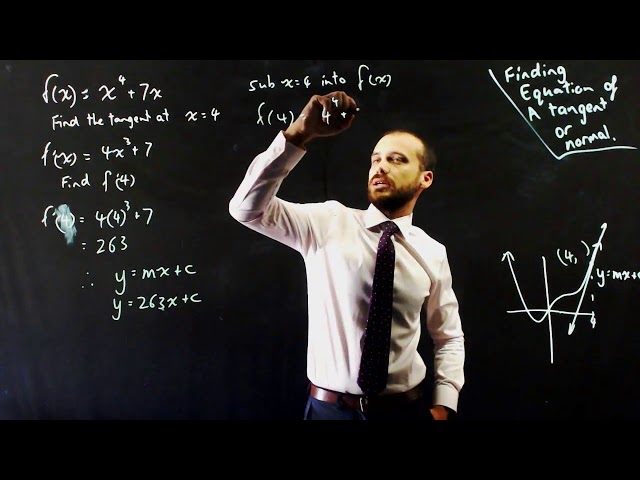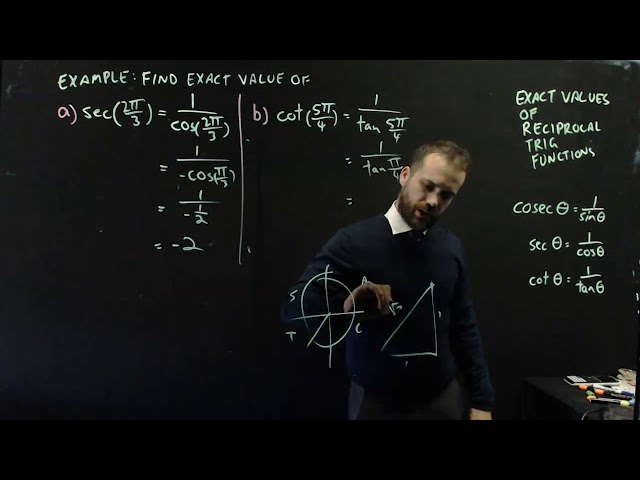Year 12
Mathematics Extension 1 (New South Wales)
ME-P1: Proof by Mathematical Induction
MA-C3: Applications of Differentiation
-

Finding Stationary points
-

Nature of Stationary points
-

Optimisation when the function is unknown
-

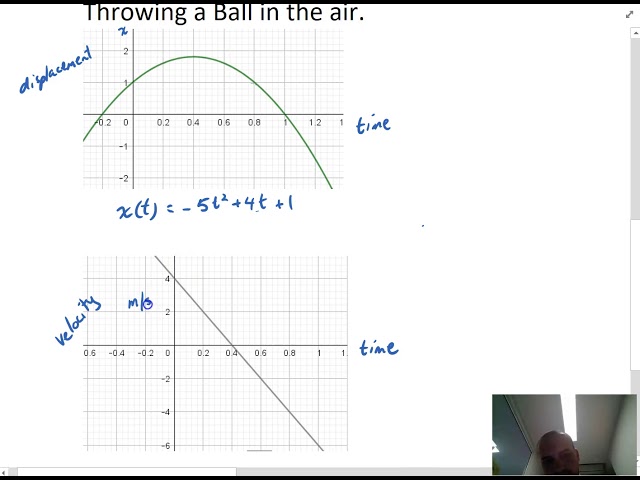
Introduction to Kinematics
-

Finding the equation of a tangent
-

Finding the equation of a normal
-

Equations of tangents and normals revisited
-

Rates of change application
-

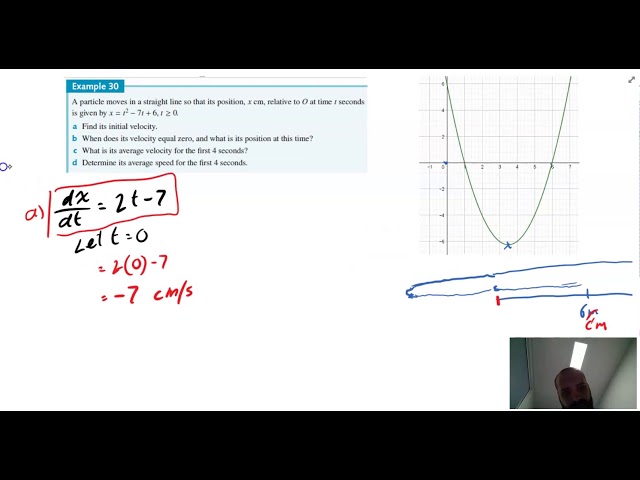
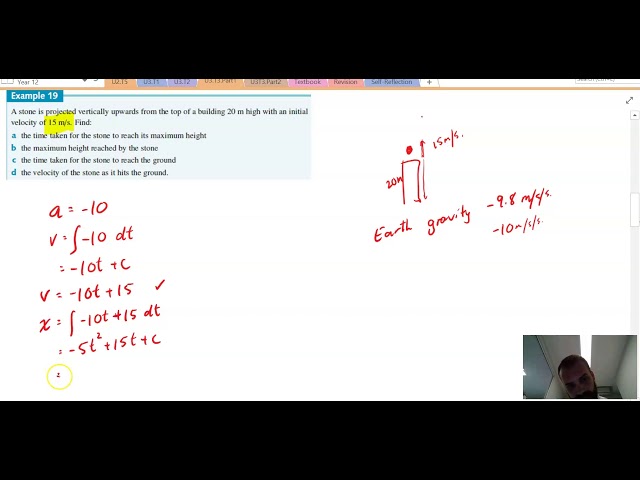
Motion in a straight line An application of rates
-

Motion in a straight line acceleration recap
-

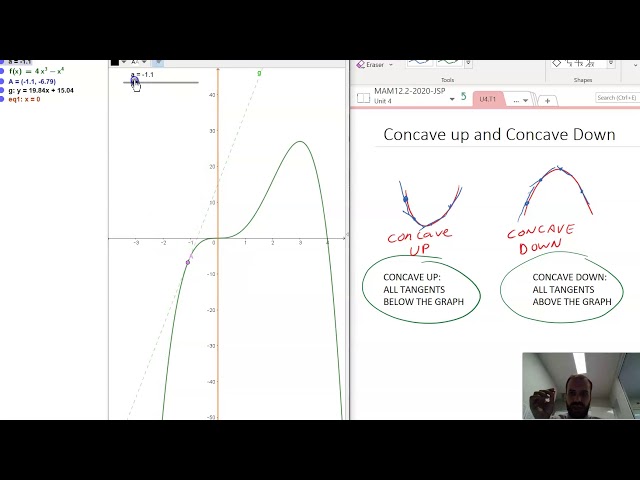
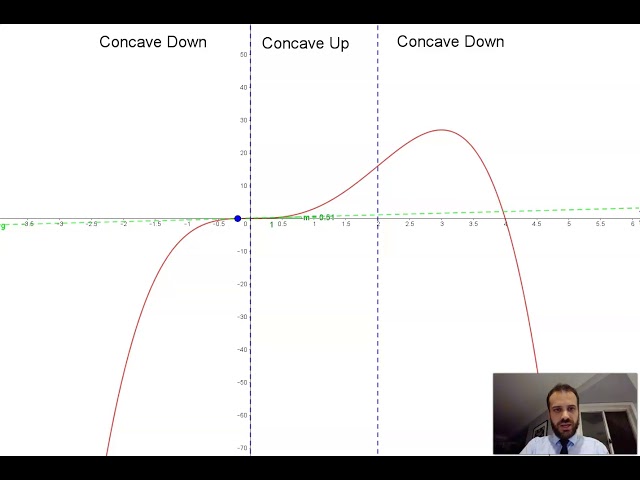
Concave up and Concave down Part 1: 2 useful definitions
-

Concave up and Concave Down Part 2 A more useful definition
-

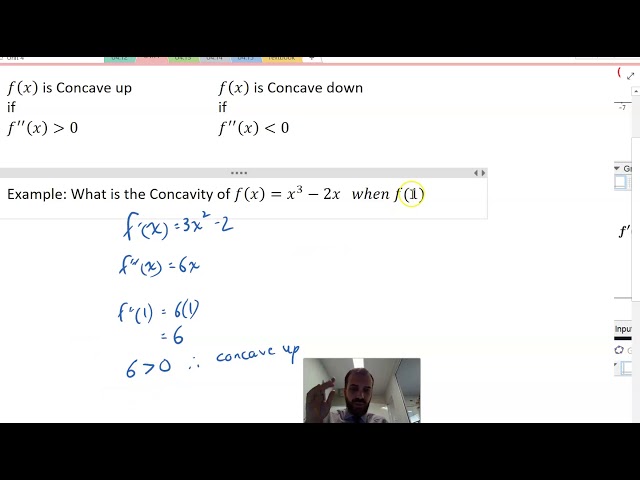
Concavity and the second derivative
-

Points of Inflection and the 2nd derivative
-

The 2nd Derivative test
-

Sketching Functions with the second derivative and Points of Inflection
-

Introduction to Kinematics
-

Applications of Integration in motion questions
-

Optimisation when the function is unknown
ME-V1: Introduction to Vectors
V1.1: Introduction to Vectors
V1.2: Further Operations with Vectors
-

Vectors finding the magnitude
-

Vectors finding the unit vector
-

Finding direction of a vector
-

Defining a vector between 2 points
-

Vector Revision part 1
-

The dot product part 1
-

The dot product part 2
-

The dot product part 3
-

The scalar product or dot product of a vector revisited
-

Force Vector Diagrams
-

Resolving Force Vectors
-

Resolving forces into their components
-

Resolving Forces into components part 2
-

Vector midpoints
-

Vectors in component form recap
-

Vectors in polar form
-

What’s a vector projection?
-

Calculating vector projections
-

Resolving a vector into components parallel and perpendicular to a second vector
-

Applications of vectors displacement and velocity
-

Applications of vectors displacement and velocity collisions
-

Applications of vectors relative velocity
-

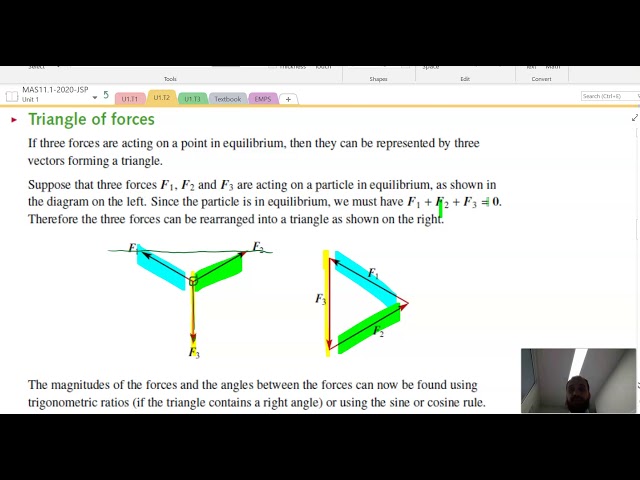
Triangle of forces
-

Inclined plane recap part 1
-

Solving equilibrium questions using resolution of forces
V1.3: Projectile Motion
-

Vector Functions Introduction and converting vector functions to cartesian functions
-

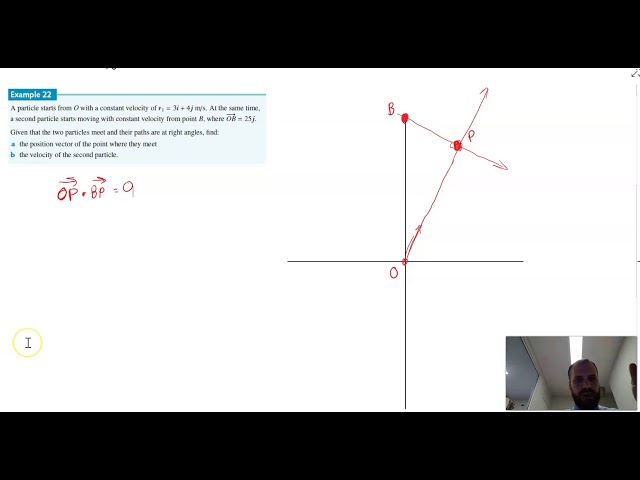
Vector equations and finding collision points
-

Vector Calculus Displacement, velocity Acceleration
-

Vector Calculus Anti differentiation worked example
-

Vector Calculus Differentiation worked examples
-

Vector Calculus Motion in a straight line
-

Vector Calculus Projectile Motion Calculating Launch Angle
ME-T3: Trigonometric Equations
-

Express the sum of trigonometric functions as a single function
-

Express the sum of trigonometric functions as a single function part 2
-

Solving trig equations of the form sin(ax+b) = c
-

Exact values of reciprocal trigonometric functions
-

Solving reciprocal trig functions
-

Proving Trigonometric identities
-

2 more pythagorean identities
-

Angle sum and difference indentities
-

Angle sum and difference identities part 2
-

Double angle identity proofs and an example
-

More proofs of trig identities
ME-C2: Further Calculus Skills
ME-C3: Applications of Calculus
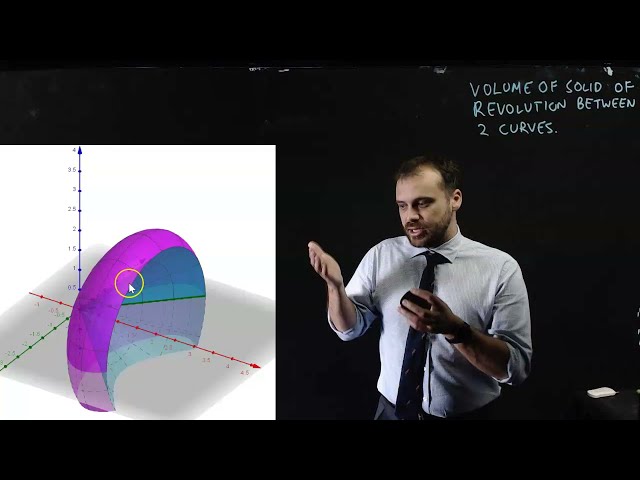
C3.1: Further Area & Volumes of Solids of Revolution
C3.2: Differential Equations
-

Implicit differentiation
-

Solving differential equations
-

Solving differential equations given in terms of f(y)
-

Setting up differential equations
-

Isaac Newton & My Cup of Coffee: Differential Equations Applications
-

Differential equations: Mixing Problems
-

Modelling Population Growth: The Logistic Equation – Differential Equations
-

Verifying solutions to differential equations
-

Separable differential equations
-

Displacement velocity acceleration etc
-

Velocity in terms of displacement Acceleration in terms of velocity
-

Other Expressions for acceleration part 1
-

Other Expressions for acceleration part 2
-

Simple Harmonic Motion
-

Resultant forces
-

Momentum
-

Newton’s laws of motion
-

Newtons laws of motion examples
-

Calculating the Normal Reaction Force in an Elevator
ME-S1: The Binomial Distribution
S1.1: Bernoulli & Binomial Distributions
-

Bernoulli sequence
-

Binomial distribution introduction
-

Developing Binomial Distribution Intuition
-

The binomial Probability Formula
-

Binomial Probability Distribution formula Worked Example
-

Binomial Probability formula at most and at least
-

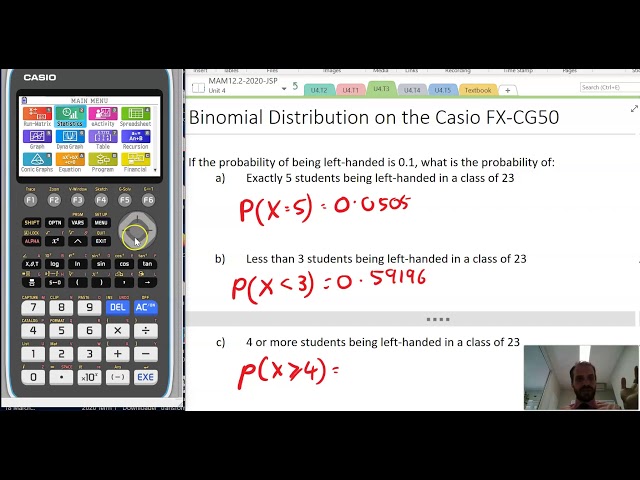
Binomial Distribution on the Casio FX CG50AU
-

Binomial Probability Conditional Probability
-

Binomial distribution expected value variance and standard deviation
-

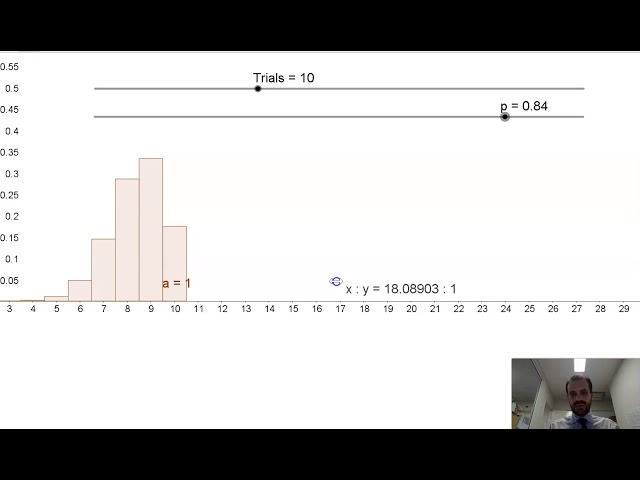
Construct a Binomial Distribution Graph
-

Binomial Distribution finding a sample size
S1.2: Normal Approximation for the Sample Proportion
-

Why is sample proportion interesting and important
-

Sampling from a small population
-

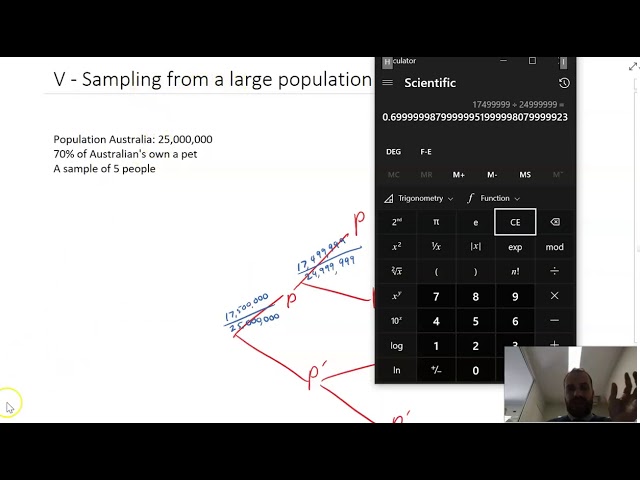
Sampling from a large population
-

Sample proportion mean and standard deviation
-

Approximating the distribution of sample proportions using the normal distribution
-

Determining required Sample size for a given Margin of error
-

Binomial Approximation to the normal and sample proportion, one question two ways