AC Maths Methods Maths Year 12

Derivatives of exponential functions – An introduction

Derivatives of exponential functions – An introduction

Derivatives of exponential functions Simple rules

Applications of derivatives of exponential Functions

Derivatives of periodic functions 1 A graphical explanation

Derivatives of Periodic functions 2 Simple examples

Derivatives of periodic functions Applications 1

Derivatives of periodic functions Applications 2

Derivatives of polynomials, negative and fractional powers by rule

Composite functions and the chain rule

The chain rule the fast way

The product rule

The quotient rule

The chain rule revisited

The Product Rule Revisited

Concave up and Concave down Part 1: 2 useful definitions

Concave up and Concave down Part 1: 2 useful definitions

Concavity and the second derivative

Points of Inflection and the 2nd derivative

The 2nd Derivative test

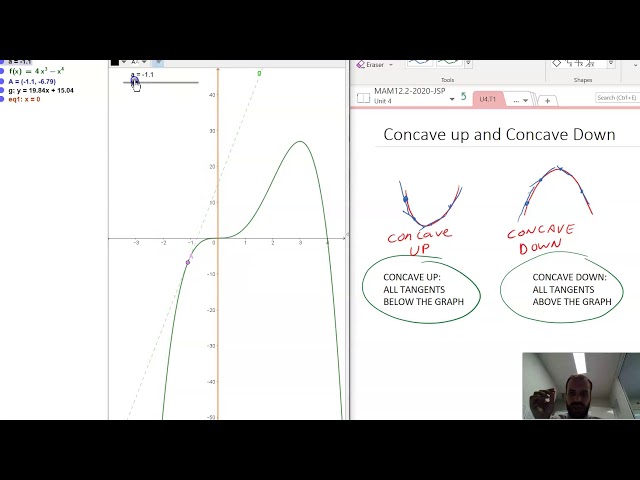
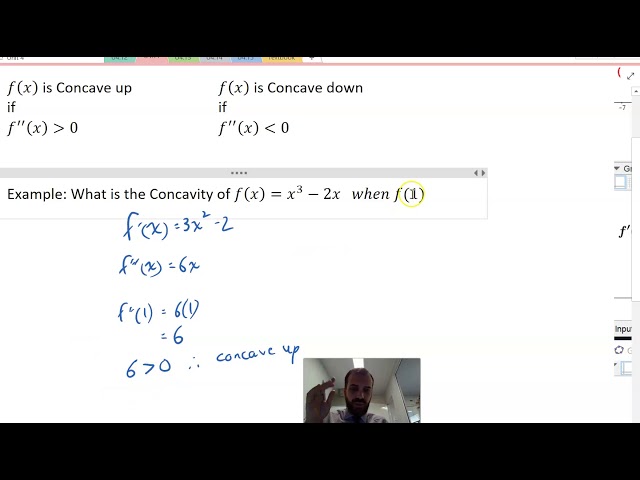
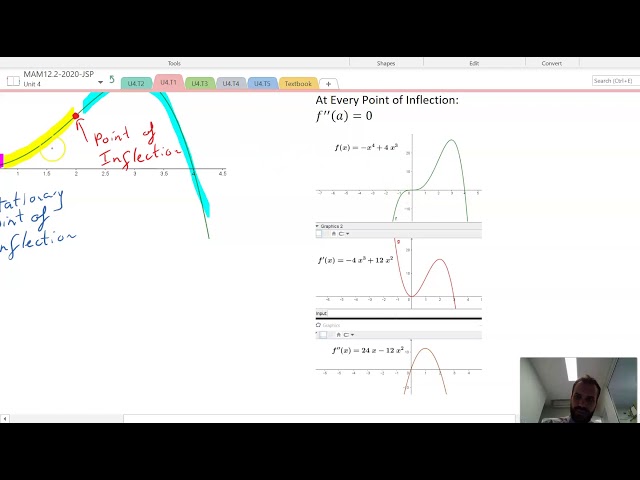
Sketching Functions with the second derivative and Points of Inflection

Introduction to Kinematics

Introduction to Kinematics

Optimisation when the function is unknown

Intro to Integration and integrating polynomials

Integration a little bit of theory

Integration finding the c value

Integration the reverse chain rule

Integration resulting in a logarithm

Integrals of exponentials

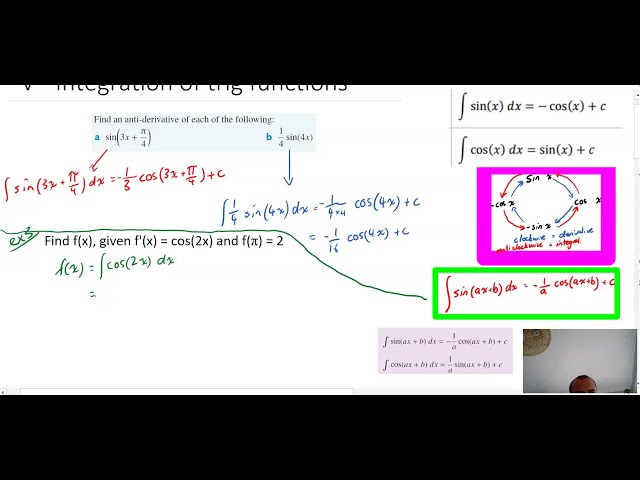
Integration of trig functions

Integration by recognition updated

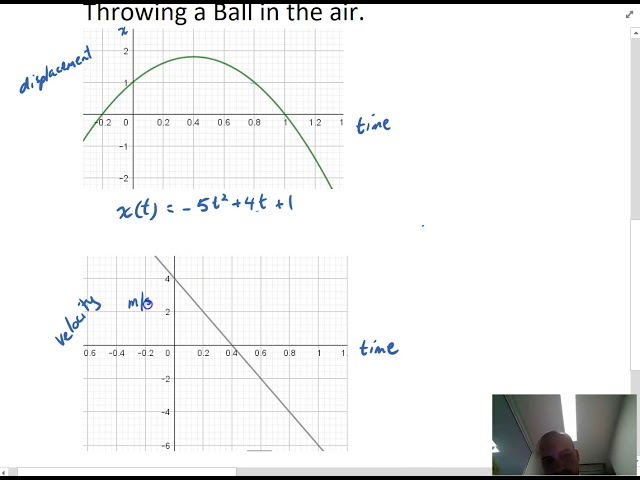
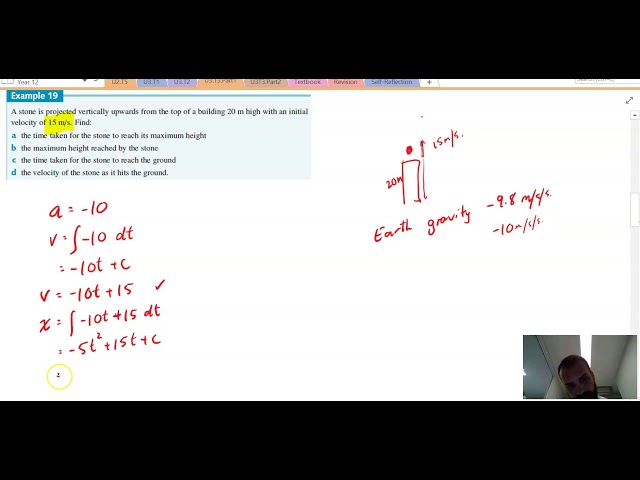
Applications of Integration in motion questions

The definite integral

The definite integral signed area

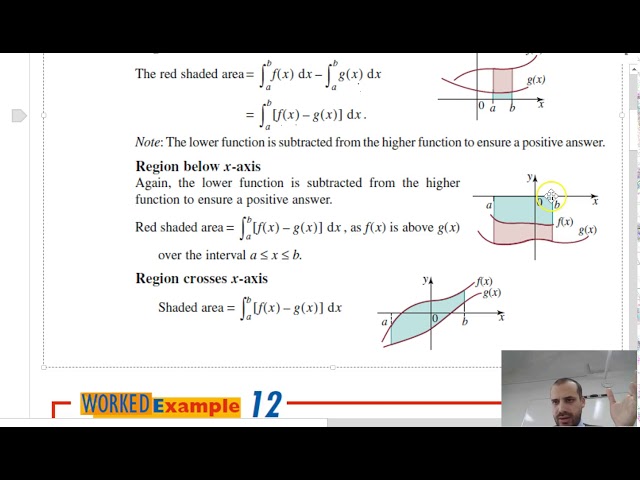
Area between two curves

The area under a derivative function

Trapezoidal Rule Fully explained

Discrete Random Variables

Discrete Random Distributions Expected value

Probability Distributions Discrete vs continuous random variables

Discrete Probability distributions 2 Properties of discrete probability distributions

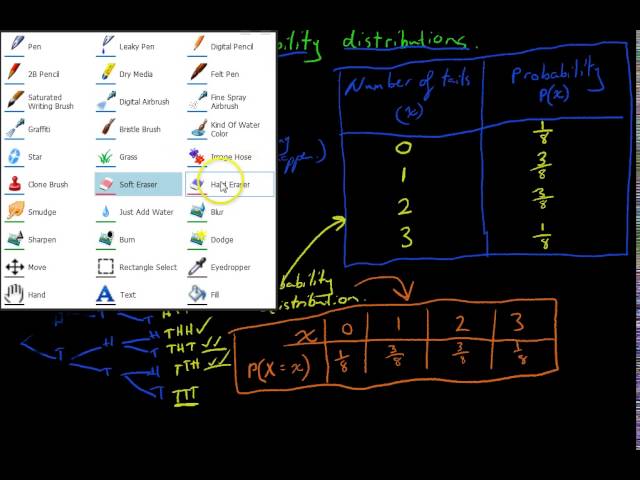
Discrete probability distribution 3 Graphing the distribution

Discrete probability distributions 4 Applications

Discrete random distributions Expected value challenging but important

Discrete Random Variables including conditional probability

how to draw Pascal's triangle

Using pascals triangle to calculate combinations

Binomial distribution Combinations

Bernoulli sequence

Binomial distribution introduction

Developing Binomial Distribution Intuition

The binomial Probability Formula

Binomial Probability Distribution formula Worked Example

Binomial Probability formula at most and at least

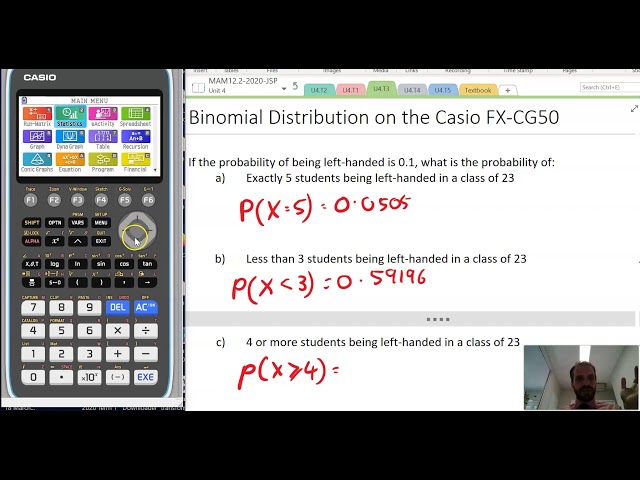
Binomial Distribution on the Casio FX CG50AU

Binomial Probability Conditional Probability

Binomial distribution expected value variance and standard deviation

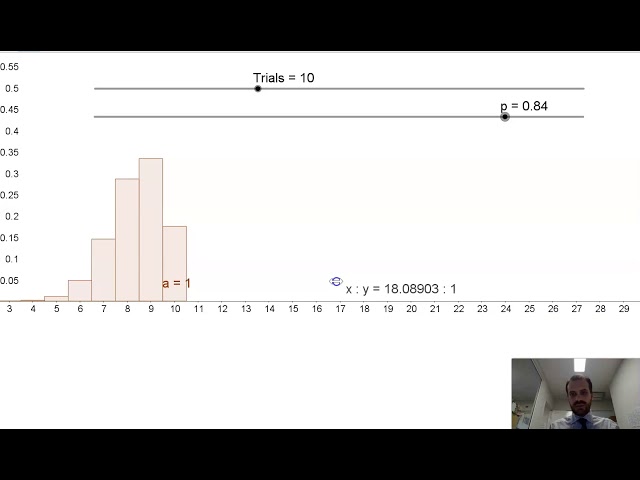
Construct a Binomial Distribution Graph

Binomial Distribution finding a sample size

Estimating probability of a continuous random variable using data

The probability Density Function

Mathematical proof that you do not exist

Calculating probability using a probability density function

Proving a function is a probability density function

unknowns in probability density functions

Unbounded Probability density functions

The mean of a continuous random variable

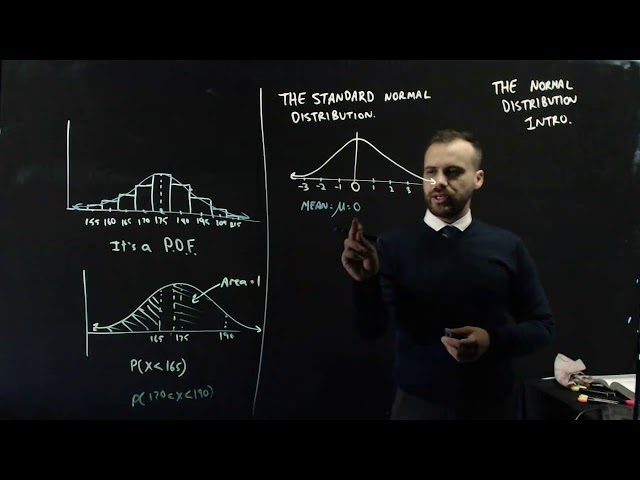
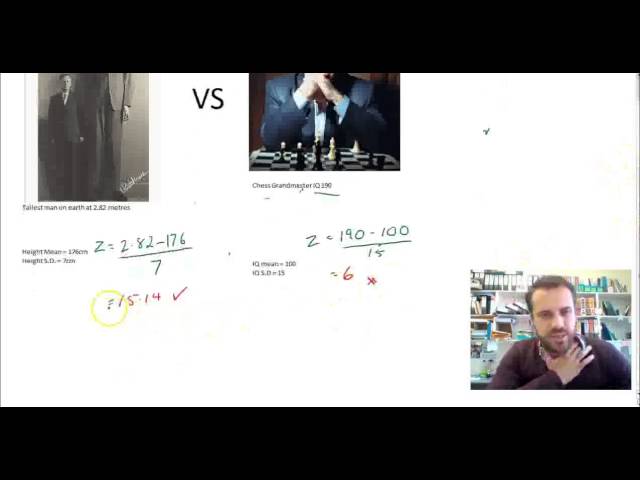
The normal distribution Introduction

Determining normal probabilities on the casio fx cg50AU

The Inverse Normal Distribution on the Casio FX CG50AU

A tricky normal distribution question

The Normal Approximation to the binomial distribution

Why is sample proportion interesting and important

Sampling from a small population

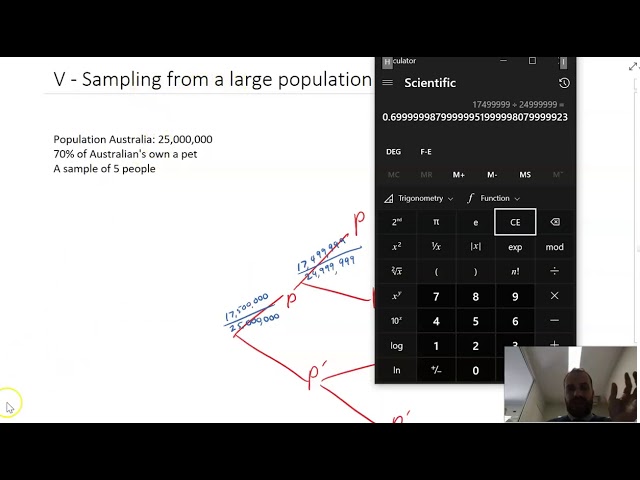
Sampling from a large population

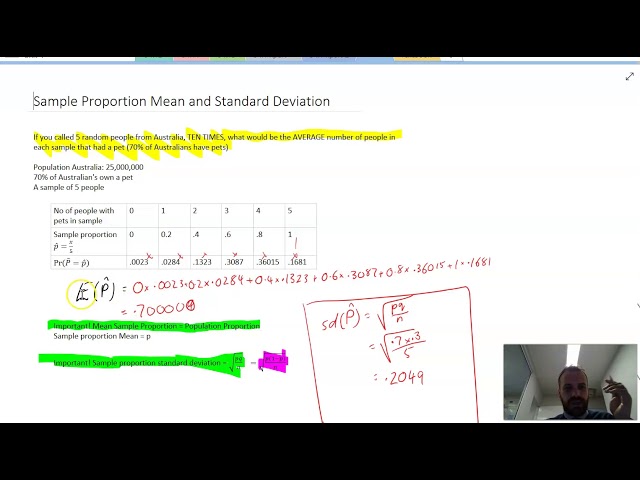
Sample proportion mean and standard deviation

Approximating the distribution of sample proportions using the normal distribution

Confidence Intervals for Population proportion

Finding a confidence interval on the Casio FXCG50 AU Calculator

Determining required Sample size for a given Margin of error

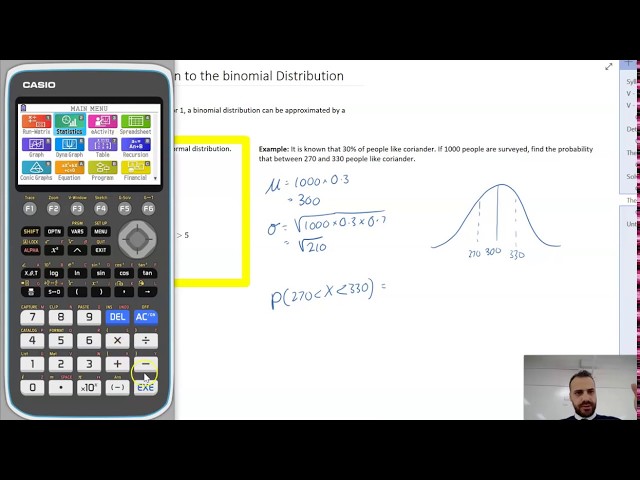
Binomial Approximation to the normal and sample proportion, one question two ways