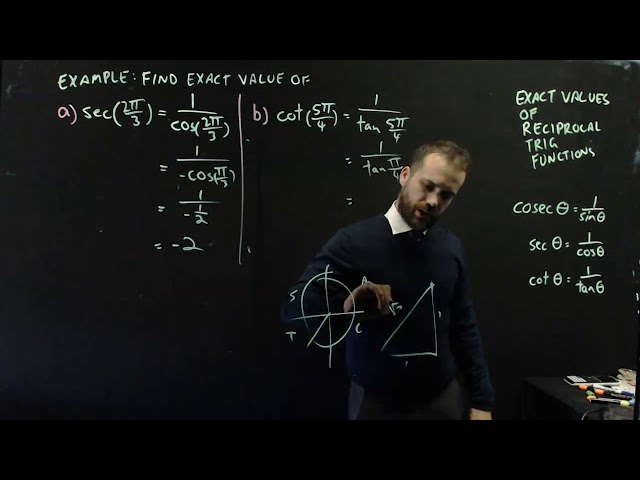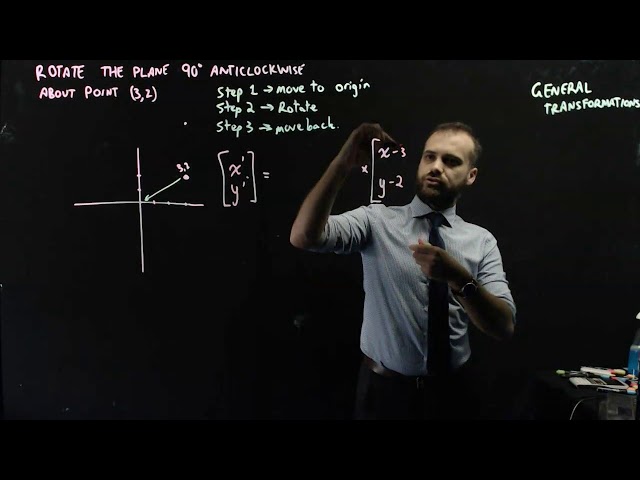Year 11
Specialist Mathematics (Australian Curriculum)
Combinatorics
-

Addition and Multiplication principles
-

Factorials!
-

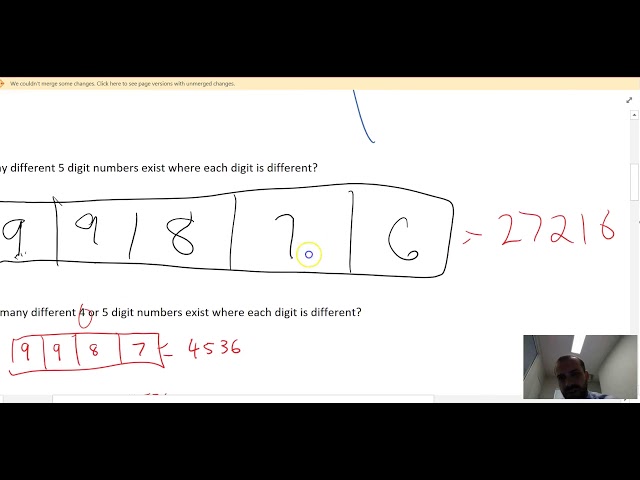
Permutations
-

Arrangements in a circle
-

Arrangements from like objects
-

Addition and multiplication principles revision
-

Factorials and permutations revision
-

Permutations of like objects
-

Permutations with restrictions
-

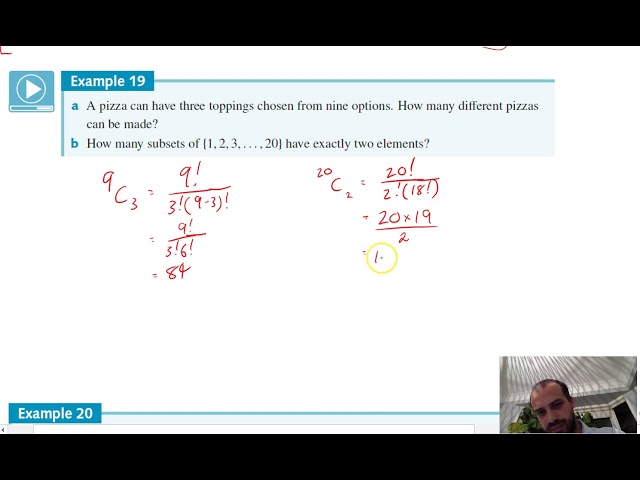
Combinations
-

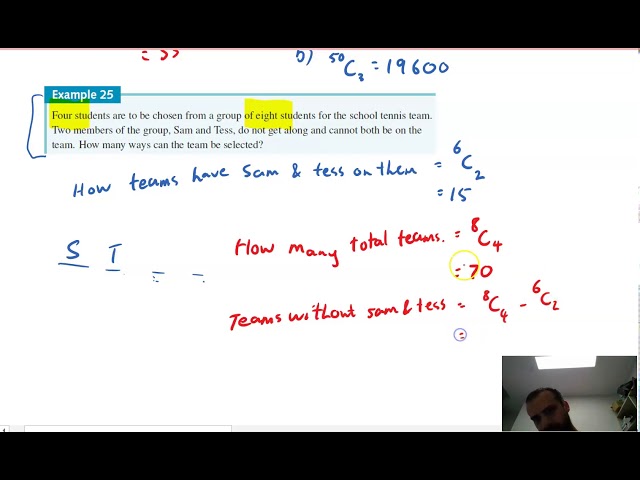
Combinations with restrictions
-

Pascals triangle and subsets of a set
-

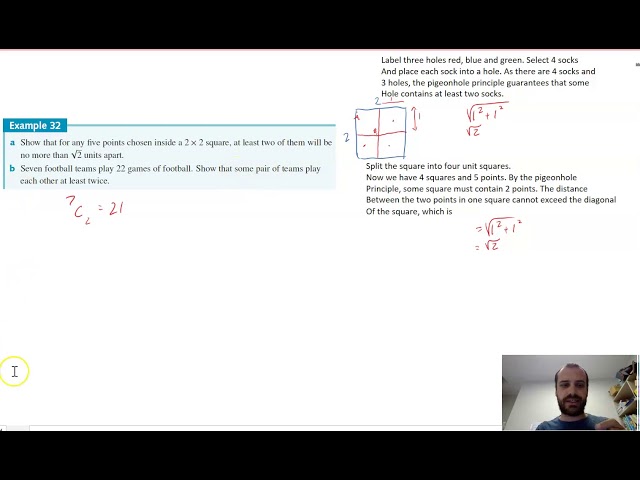
Pigeonhole principle
-

Basic Set Theory
-

The inclusion exclusion principle for 2 and 3 sets
Vectors in the Plane
-

Vectors Introduction
-

Adding Vectors Graphically
-

Vectors Multiplying by a scalar
-

Vectors in 2D and 3D Shapes
-

Vectors in component form
-

Adding Vectors in component form
-

Vectors multiplying by a scalar in component form
-

Vectors finding the magnitude
-

Vectors finding the unit vector
-

Defining a vector between 2 points
-

Finding direction of a vector
-

Force Vector Diagrams
-

Resolving Force Vectors
-

Resolving forces into their components
-

Resolving Forces into components part 2
-

Vector Revision part 1
-

Vector midpoints
-

Vectors in linear combinations
-

Vectors in component form recap
-

Vectors in polar form
-

The scalar product or dot product of a vector revisited
-

What’s a vector projection?
-

Calculating vector projections
-

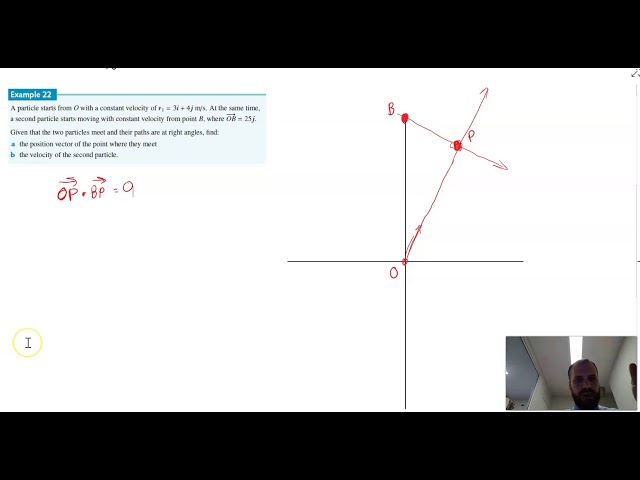
Applications of vectors displacement and velocity
-

Applications of vectors displacement and velocity collisions
-

Applications of vectors relative velocity
-

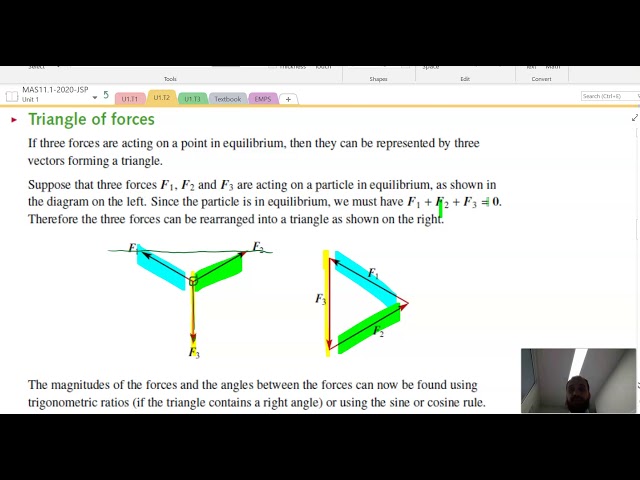
Triangle of forces
-

Inclined plane recap part 1
-

Solving equilibrium questions using resolution of forces
-

Resolving a vector into components parallel and perpendicular to a second vector
Geometry
Trigonometry
-

Trigonometry: Unit circle revision done fast
-

Solving trig equations of the form sin(ax+b) = c
-

Pythagorean identity
-

Pythagorean identity rearrangement
-

Using Pythagorean Identities Part 1
-

The general solution of trigonometric equations
-

Sketching Tan Functions
-

Reciprocals of Trigonometric Functions
-

Transformations of the reciprocal Trigonometric functions
-

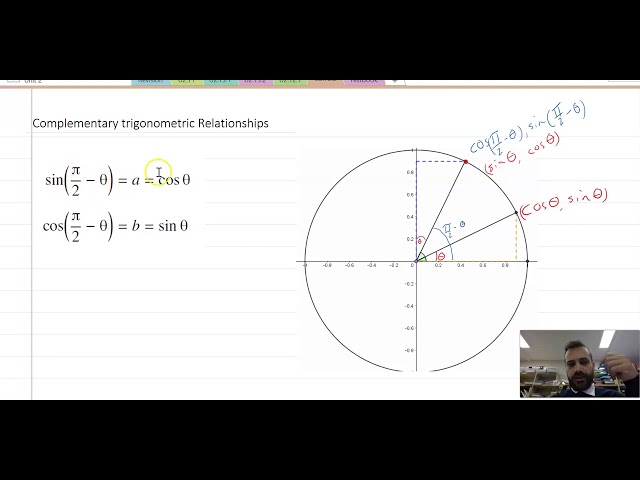
Complementary Trigonometric Relationships
-

Exact values of reciprocal trigonometric functions
-

Solving reciprocal trig functions
-

The pythagorean Identity and reciprocal trigonometric functions
-

Proving Trigonometric identities
-

2 more pythagorean identities
-

Angle sum and difference indentities
-

Angle sum and difference identities part 2
-

Double angle identity proofs and an example
-

More proofs of trig identities
-

Express the sum of trigonometric functions as a single function
-

Express the sum of trigonometric functions as a single function part 2
-

Product Sum Trigonometric Identities
Matrix Arithmetic
-

What is a matrix
-

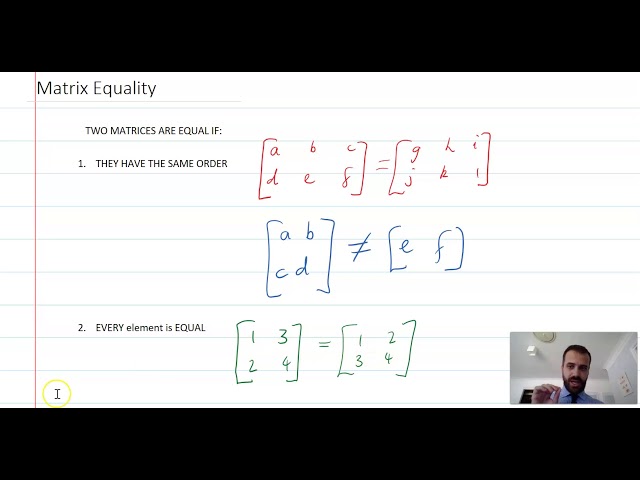
Matrix Equality
-

Storing Information in Matrices
-

Adding and subtracting matrices
-

Multiplying matrices by a scalar
-

Multiplying Matrices the better way
-

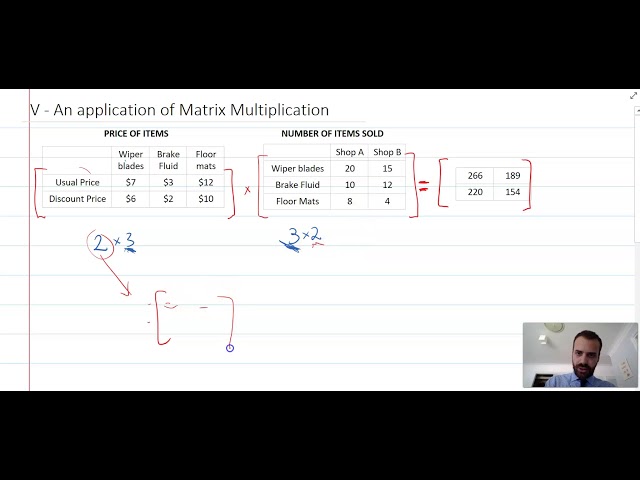
An Application of Matrix Multiplication
-

Powers of Matrices
-

The Identity Matrix
-

Matrices Recap
-

Solving Matrix equations using the multiplicative inverse
-

Simultaneous equations using matrices
-

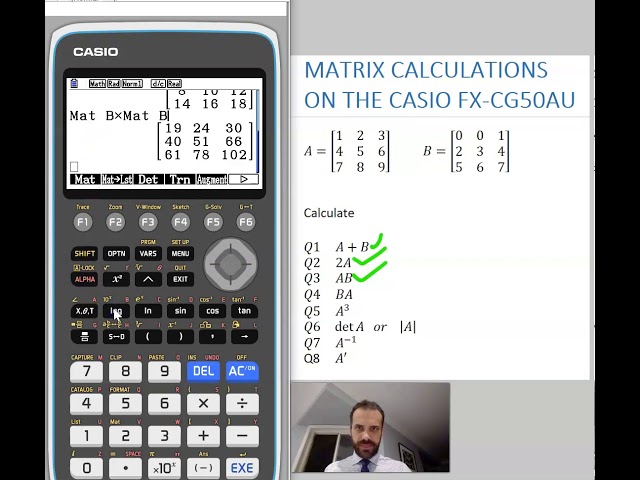
Matrix Calculations on the Casio FX-CG50AU
Transformations in the Plane
-

Transformations in one dimensional space A different to think about mathematical operations
-

Linear Transformations Introduction
-

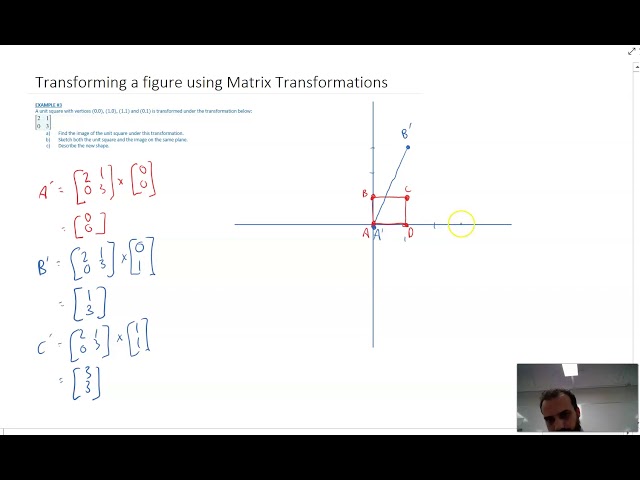
Transforming a figure using Matrix Transformations
-

What is actually happening in a linear transformation
-

Dilation transformations Using Matrices
-

Shear Transformations Using Matrices
-

Reflections in the x and y axis using Matrix Transformations
-

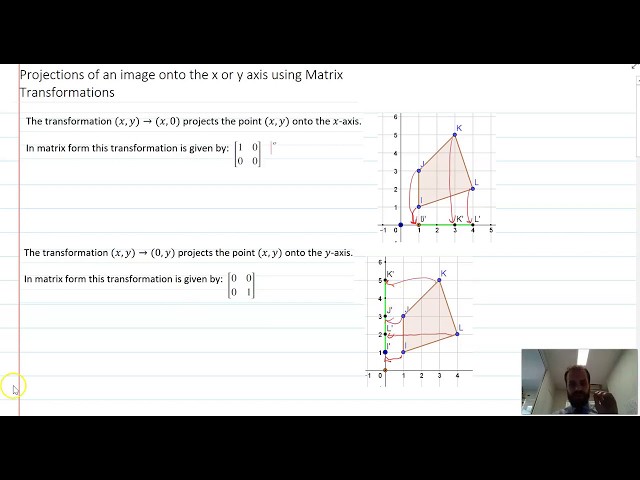
Projections of an image onto the x axis or y axis using Matrix Transformations
-

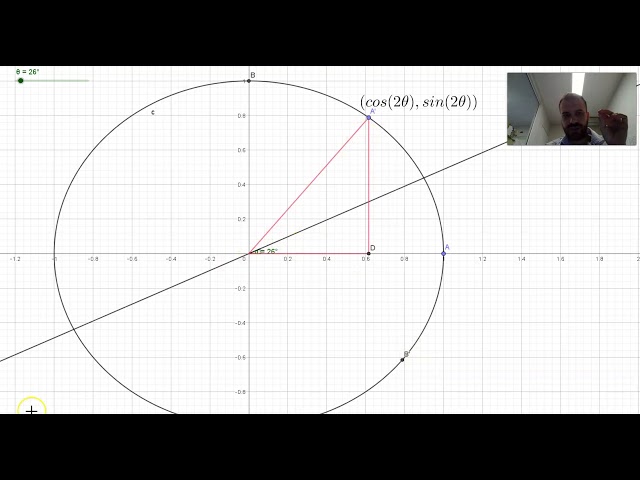
Rotations about the Origin Using Matrices
-

Reflect an object in y= x and y = -x using Matrix Transformations
-

Reflecting in the line y = mx with Matrix Transformations
-

Composition of Matrix Transformations
-

Inverse Matrix Transformation
-

Transforming multiple points using a single matrix transformation
-

Transforming relations using matrices part 1
-

Transforming relations using matrices part 2
-

Transforming relations no shortcuts
-

Transforming relations using matrices part 3
-

Finding an unknown matrix of transformation
-

Equation of ellipses crash course
-

Finding area of a transformation using the determinant
-

General Transformations part 1
-

General Transformations part 2
Real & Complex Numbers
-

Intro to complex numbers
-

Working with imaginary and complex numbers
-

Powers of i
-

Simplifying with powers of i
-

Adding and subtracting complex numbers
-

Multiplying complex numbers by a constant
-

Multiplying complex numbers by each other
-

Equality of complex numbers
-

Complex Numbers The Recap
-

Complex number conjugates
-

The multiplicative inverse of a complex number
-

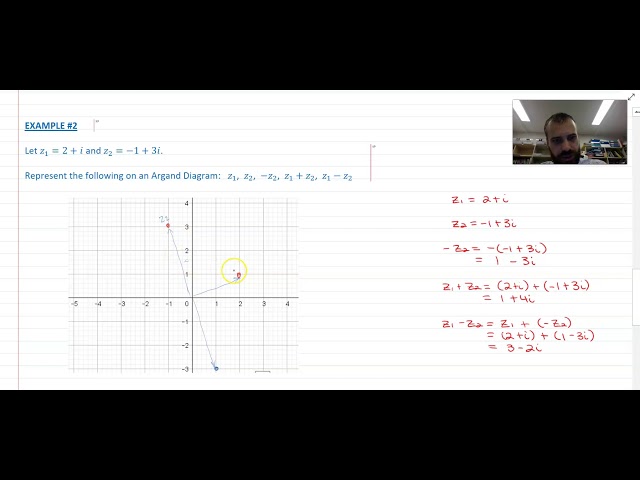
Argand Diagrams What complex numbers and Vectors have in common
-

Solving equations with complex numbers
-

Completing the square with complex numbers
-

Polar Form of a complex number
-

Polar form Multiplication and division of complex numbers
-

De Moivres theorem raising complex numbers to a power